Question
Find the amount of energy given to the nucleus and to the ray in the reaction , using the conservation of momentum principle and taking the reactants to be initially at rest. This should confirm the contention that most of the energy goes to the ray.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 40 (Problems & Exercises)
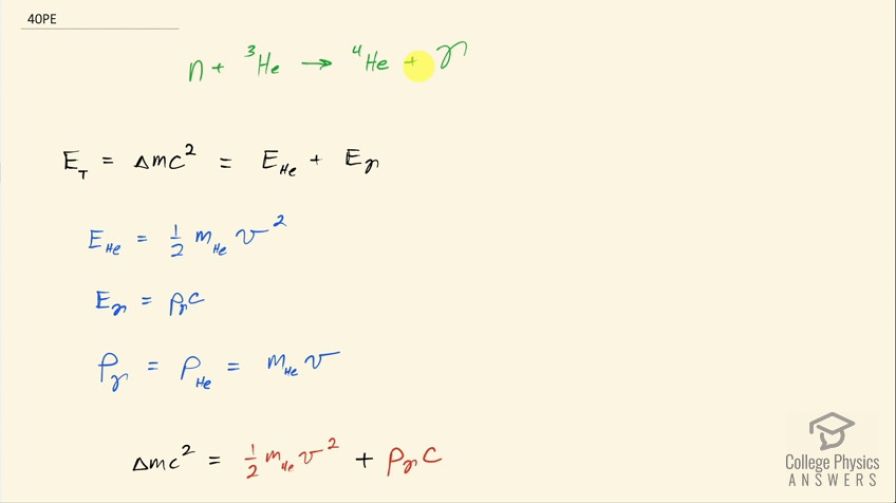
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
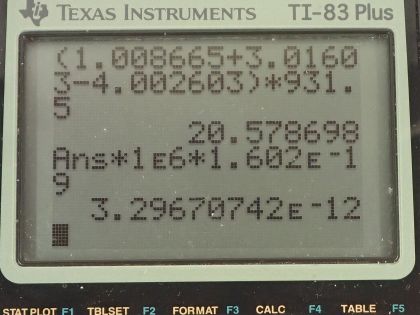
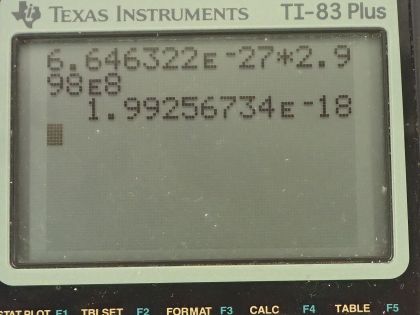
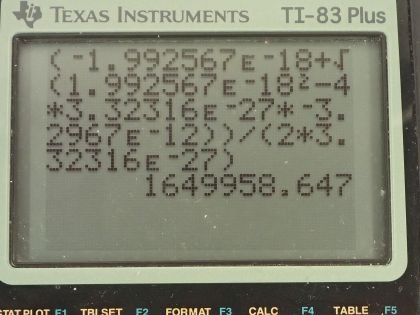
This is College Physics Answers with Shaun Dychko. In the fusion of a neutron to a helium-3 nuclide and it turns into a helium-4 nuclide and a gamma ray, we want to figure out what is the energy given to the helium nuclide and what is the energy given to the gamma photon? So we are going to say that the total energy that they share, is equal to the difference in mass between the left side and the right side times c squared and this will be the energy given to the helium plus the energy given to the gamma particle and I am writing just helium here but I am referring to the helium-4 here. The helium-3 is at rest initially we are told and so is the neutron. Okay! So the helium nuclide will have an energy of one-half times its mass times its speed squared— we're assuming non-relativistic speeds here— and we'll see later that that's a reasonable assumption based on the energy released in this reaction being much less than the mass energy of the helium nuclide. The energy of the gamma photon is its momentum times its speed of light and the momentum of the gamma photon has to equal the magnitude of the momentum of the helium nuclide since there are only 2 of them and so they have to be going in opposite directions with momenta that are of equal magnitude in order to have a total momentum of zero as they must have since the initial two particles had a total momentum of 0. Okay! So that means momentum of this photon then we can say is the mass of the helium nuclide times its velocity. So let's do some substitution now: we have this total energy released in the reaction equals one-half mass of the helium times its speed squared plus momentum of the photon times speed of light and that's substituting for the energy terms here from here and here and then substitute further yet by replacing momentum of the photon with mass of the helium times its speed and now we have a quadratic equation with the only unknown being the speed of the helium nuclide and we are going to solve for that in a second. First let's put everything on one side and then say equals 0 and then we can see how the different terms correspond to our traditional formula down here. Okay! So we want to have this equation in the form of some coefficient times the squared term plus some other coefficient times the linear term to the power of 1 plus some constant term equals 0. Okay! So first let's figure out what is this Δmc squared? So that's going to be the mass of a neutron plus the mass of a helium-3 atom minus the mass of a helium-4 atom times c squared and these atomic masses each have two electron masses included in them and we don't want any electron masses here but since there are 2 in the helium-3 and 2 also in the helium-4, those two electron masses subtract away so we don't have to worry about them. And this neutron and the helium-3 are from the left side and then the helium-4 is on the right side and the gamma particle has no mass. Okay! So looking up the mass of a neutron in atomic mass units and then this is the atomic mass of helium-3 and then here is minus the atomic mass of helium-4 and then multiply by 931.5 megaelectron volts per c squared for every atomic mass unit and then multiply by c squared, we get 20.5787 megaelectron volts. We are going to convert this into joules by multiplying by 1.602 times 10 to the minus 19 joules per electron volt but then I also have to multiply by 10 to the 6 electron volts for every megaelectron volt leaving us with joules here that's 3.2967 times 10 to the minus 12 joules; I am choosing units that are mks units and then we'll get an answer for speed in meters per second. So that takes care of this term; we also want to know what is the mass of the helium nuclide in kilograms? So we multiply its atomic mass by 1.6605 times 10 to the minus 27 kilograms per atomic mass unit and this is 6.646322 times 10 to the minus 27 kilograms. so that's what we substitute in here for mass of the helium and then also here multiplying by speed of light because that's what we have here— c for speed of light— and then minus the energy released in the reaction in joules. Then taking the product of these two makes this number here and then this times a half makes this coefficient here and now we finally have our equation in the form of ax squared plus bx plus c, where x is the speed v that we want to find. And we have a formula for solving a quadratic equation negative of the linear coefficient plus or minus square root of the linear coefficient squared minus 4 times the quadratic coefficient times the constant term divided by 2a. Alright! So the speed then is negative of this number plus or minus that number squared— this being the coefficient of the unknown to the power of 1— minus 4 times a, which is the coefficient of the term of the variable squared times c and which is negative— pay attention to that negative there— that's negative 3.2967 times 10 to the minus 12— that's the energy released— and divided by 2 times the coefficient of the speed squared, this works out to 1.64996 times 10 to the 6 meters per second so now we have the speed of the helium nuclide and its energy would be one-half times its mass in kilograms times its speed squared and then convert those joules into megaelectron volts because it makes it easier to compare things when they all have the same units. So we have total energy released of 20.5787 megaelectron volts so we want to have this in megaelectron volts as well in order to compare with the total energy released and to compare with the energy of the gamma photon. So converting from joules into megaelectron volts gives us 0.0565 megaelectron volts of energy for the helium nuclide the helium-4 nuclide after, which is a product of this reaction. The energy for the gamma photon then is the total energy released in the reaction minus whatever is used up for the helium nuclide so that's 20.5787 megaelectron volts minus 0.0565 megaelectron volts and that is 20.52 megaelectron volts. So this is three orders of magnitude or four orders of magnitude bigger than the energy for the photon... or sorry... than the energy of the helium nuclide so most of the energy goes through the photon and there we go!