Question
The activities of and used in thyroid scans are given in Table 32.1 to be and , respectively. Find
and compare the masses of 131 I and 123 I in such scans,
given their respective half-lives are 8.04 d and 13.2 h. The masses are so small that the radioiodine is usually mixed with stable iodine as a carrier to ensure normal chemistry and distribution in the body.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 6 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
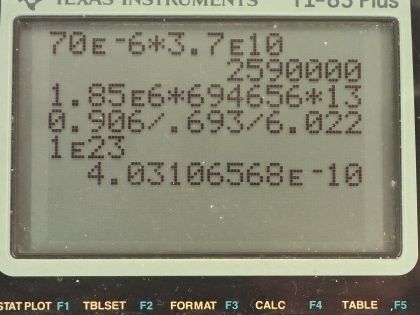
This is College Physics Answers with Shaun Dychko. Our job in this question is to calculate what mass of iodine-131 or iodine-123 are used in thyroid scans? We are told that the activity of iodine-131 is 50 microcuries, which we convert into becquerels by multiplying by 3.70 times 10 to the 10 becquerels per curie after converting the microcuries into curies and that is 1.850 times 10 to the 6 becquerels We convert the activity of iodine-123, which is 70 microcuries into becquerels and you can see that this question involves a lot of bookkeeping so let's take care of all this bookkeeping stuff at the beginning here so we don't have to convert units in our formulas. So we have the atomic or the molar mass of iodine-131 is 130.906 grams per mol and we look that up in the appendix at the end of the textbook here and then for iodine-123, we have to take a bit of a guess and use this iodine-127 molar mass and subtract from it the molar mass of four nucleons because this is iodine-123 which is 4 less than 127. So that's 122.904 grams per mol is our estimated atomic mass for iodine-123. The half-lives we convert into seconds so we are given 8.04 days is a half-life of iodine-131 we multiply by 24 hours per day and then by 3600 seconds per hour and we have 694656 seconds and the half-life of iodine-123 is converted from 13.2 hours into 47520 seconds. Well alright! With all that taken care of, let's get into the algebra here we are trying to figure out the mass remember so we know that activity is 0.693 multiplied by the number of atoms divided by the half-life of that atom so I have a subscript 131 here to say that we are dealing with iodine-131 initially. So the number of atoms of iodine-131 will be the mass of iodine-131 divided by the molar mass multiplied by Avogadro's number. So we substitute all of this in place of N and then we have the activity of 131 then is 0.693 times the mass times Avogadro's number divided by the molar mass divided by half-life and then clean that up in and write it like this by putting this molar mass in the denominator... we can multiply top and bottom by this to put it there. So the next step is to solve for this mass. We will multiply both sides by half-life of 131 and then by the molar mass of iodine-131 and divide both sides by 0.693 and divide by Avogadro's number so we do that here and we also do it here. So then the mass is all of this here: we have the activity—1.850 times 10 to the 6 becquerels— times the half-life of iodine-131 times the molar mass of iodine-131 divided by 0.693 times Avogadro's number and that's 4.0 times 10 to the minus 10 grams which is an astonishingly small mass and it's amazing that they can control a mass this small and select this particular amount for a patient. So the mass of iodine-123 will be the same formula but now we are plugging in all the values corresponding to iodine-123. So you have the activity times the half-life of iodine-123 times the molar mass divided by 0.693 times Avogadro's number and that's 3.6 times 10 to the minus 11 grams.