Question
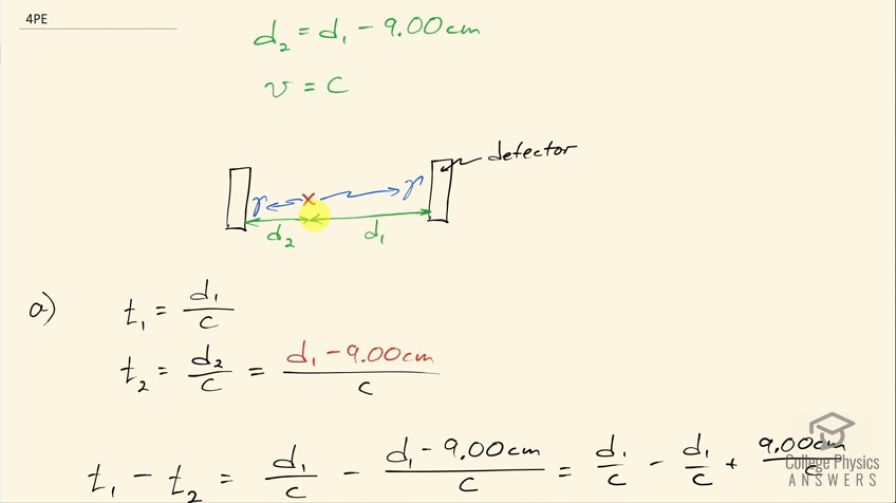
(a) Two annihilation rays in a PET scan originate at the
same point and travel to detectors on either side of the patient. If the point of origin is 9.00 cm closer to one of the detectors, what is the difference in arrival times of the photons? (This could be used to give position information, but the time difference is small enough to make it difficult.)
(b) How accurately would you need to be able to measure arrival time differences to get a position resolution of 1.00 mm?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 4 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Two annihilation gamma rays are produced in a positron emission tomography scan and the distance to one detector is 9.00 centimeters less than the distance to the other detector so the annihilation occurred here and gamma rays are emitted directly opposite each other, which is always going to be the way it happens because of conservation of momentum and so the question is what is the time difference between detection of the gamma ray between these two different detectors? So the speed of the γ-ray is c because this γ-ray is an example of electromagnetic radiation, which travels at the speed of light. So the time that this gamma ray number one takes to get from the position of annihilation to this detector here is the distance it travels—d 1— divided by the speed—c— and the time for the second gamma ray is d 2 over c but d 2 is 9.00 centimeters less than d 1 we are told. So the difference in times then is t 1 minus t 2 so that's d 1 over c minus d 1 minus 9.00 centimeters over c and then divide the c into both terms in the numerator there and we have d 1 over c minus d 1 over c plus 9.00 centimeters over c. And these two terms make zero and the difference in time then is the difference in distance to the two detectors 9.00 times 10 to the minus 2 meters— converting this 9.00 centimeters into meters— and dividing that by the speed of light and that's 0.300 nanoseconds. Part (b) is saying suppose you want to have a spatial resolution of 1.00 millimeter, which is 1.00 times 10 to the minus 3 meters, what would the time difference be in that case? So we want to know if, you know, the one detector is closer to this position of annihilation than another by 1.00 millimeter, what's the time difference going to be then? So we can see that the difference in distance is the numerator and we divide that by the speed of light so we have 1.00 times 10 to the minus 3 meters divided by speed of light and that's 3.34 picoseconds.
