Question
Neutrons from a source (perhaps the one discussed in the
x-ray series) bombard natural molybdenum, which is 24 percent . What is the energy output of the reaction
? The mass of is given in Appendix A: Atomic Masses, and that of is 98.907711 u.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 2 (Problems & Exercises)
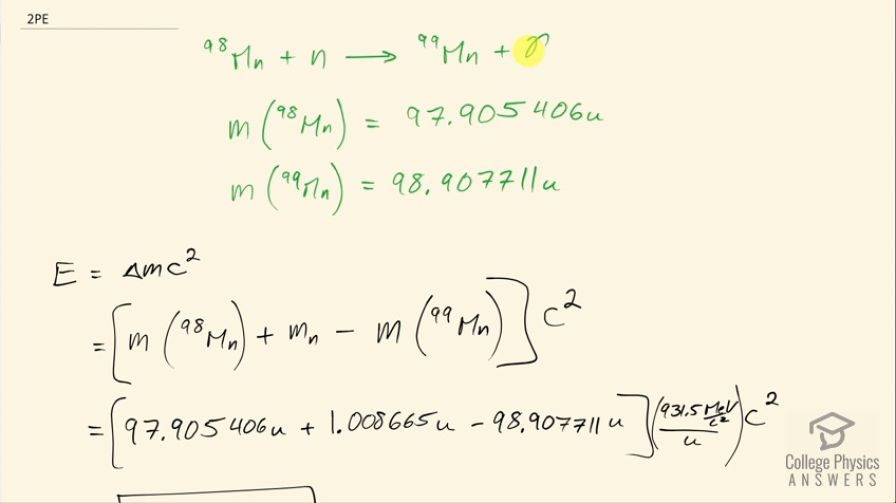
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Molybdenum-98 is being bombarded with neutrons to turn it into molybdenum-99 and this reaction also produces a gamma ray. We want to find the energy released in the reaction so we need to know the atomic mass of molybdenum-98, which we look up in the appendix at the end of the textbook and it is 97.905406 atomic mass units and we are told that molybdenum-99 has an atomic mass of 98.907711 atomic mass units. The energy released is the change in mass with a difference in mass between the products and the reactants and multiplied by c squared so that is the atomic mass of molybdenum-98 plus the mass of this neutron minus the atomic mass of molybdenum-99. Now this is a nuclear reaction which means we don't want to have electron masses included in our calculation and these atomic masses do include the masses of the electrons that surround the nuclei but that's okay because they each have the same number of electrons so molybdenum's atomic number is 42 so that means there's 42 electron masses included here but then we subtract away 42 electron masses here and so the electron masses don't matter. Alright! So we have the atomic mass of molybdenum-98 plus the mass of a neutron minus molybdenum-99's atomic mass multiplied by 931.5 megaelectron volts per c squared for every atomic mass unit and multiply that by c squared and we get 5.924 megaelectron volts of energy released.
