Question
The annual radiation dose from in our bodies is
0.01 mSv/y. Each decay emits a averaging 0.0750
MeV. Taking the fraction of to be of
normal , and assuming the body is 13% carbon, estimate the fraction of the decay energy absorbed. (The rest escapes, exposing those close to you.)
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 24 (Problems & Exercises)
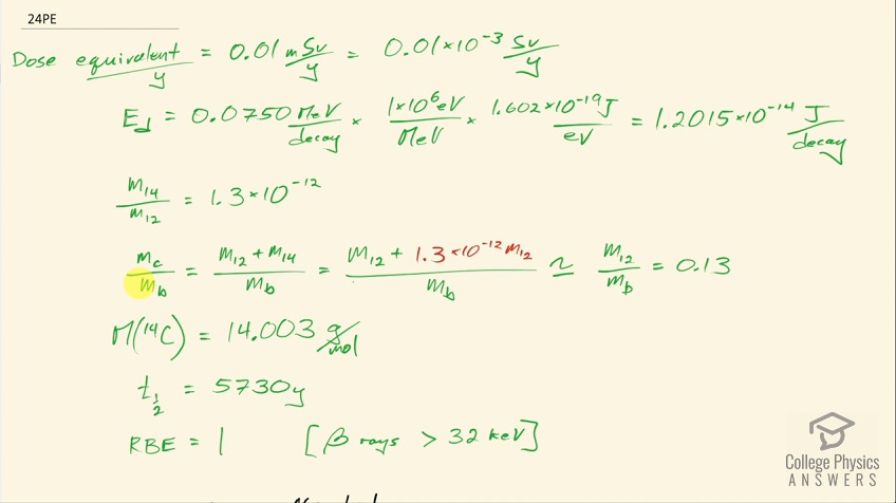
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
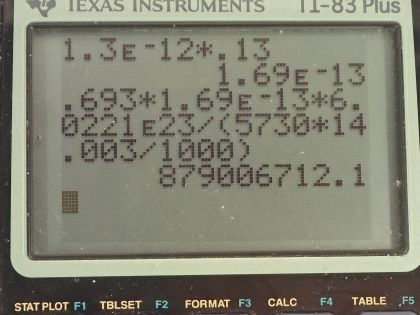
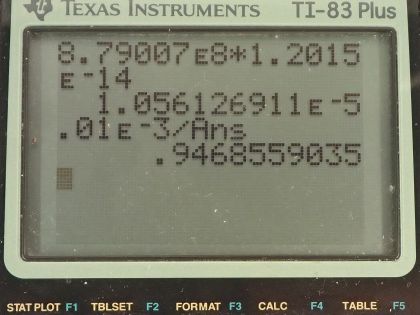
This is College Physics Answers with Shaun Dychko. We are going to figure out what fraction of the energy from carbon-14 decay in the body is absorbed? So we are told that there's a dose equivalent per year of 0.01 millisieverts every year from carbon-14 decay and the energy per decay is 0.0750 megaelectron volts and we convert that into joules so that's 1.2015 times 10 to the minus 14 joules per decay. The fraction of carbon-14 to carbon-12— this is the mass of carbon-14 to the mass of carbon-12— that fraction is 1.3 times 10 to the minus 12 and the fraction of carbon total to the mass of the body is 0.13 or 13 percent of the body is carbon, in other words. and I wrote this total mass of carbon as mass of the isotope-12 plus the carbon-14 isotope mass but this carbon-14 isotope mass is 1.3 times 10 to the minus 12 times the carbon-12 mass after rearranging this fraction here and this term is basically negligible because our precision in this fraction is only to the hundredths place and this like in the... well, you know... thousandth of a billionth place so we'll just call this the mass of carbon-12 to the mass of the body. Okay! So the molar mass of carbon-14 is 14.003 grams per mol and the carbon-14 half-life is 5730 years and the relative biological effectiveness for beta rays that have this energy greater than 32 kiloelectron volts which this does because the energy here is 75.0 kiloelectron volts the RBE is 1. There we go... that's the setup! So written down all the information we know or looked up the other things that we need and then let's get to work! The efficiency of absorption is the energy absorbed divided by however much energy is produced. The energy absorbed is fairly straightforward to figure out because we are given this dose equivalent and so the energy absorbed is the dose absorbed times the mass of the body so m subscript b is the mass of the body and dose equivalent we know is dose absorbed multiplied by the relative biological effectiveness and so we can divide both sides by RBE to get the dose absorbed and so the dose absorbed is this dose equivalent that we are told divided by RBE and that means the energy absorbed then is this fraction times the mass of the body. So that's 0.01 times 10 to the minus 3 sieverts per year multiplied by let's say a time of 1 year divided by RBE of 1 times mass of the body. So that's 0.01 times 10 to the minus 3 joules per kilogram multiplied by mass of the body. So that's the energy absorbed. We don't know what the mass of the body is so we can't turn this into joules but it turns out that the mass of the body is going to cancel because we will have this factor in our energy produced expression as well. So the energy produced is the activity in the body so this is the rate of decay of carbon-14 multiplied by some amount of time, which we'll take to be a year and then multiplied by the energy per decay. So the activity is 0.693 multiplied by the number of atoms of carbon-14 divided by carbon-14's half-life. So that's 0.693 times the mass of carbon-14 divided by the molar mass of carbon-14 multiplied by Avogadro's number. This is a substitution for N because we have grams divided by grams per mol so this fraction gives us mols and then this Avogadro number is the number of nuclei per mol and so that gives the number of nuclei, or the number of atoms. And cleaning this up by putting this molar mass in the denominator, we have 0.693 times mass of carbon-14 times Avogadro's number divided by half-life times molar mass. Now the mass of carbon-14 we can express in terms of the mass of the body and that's where we get this m subscript b factor in our energy produced which will then cancel because we are going to divide energy absorbed by this energy produced. So mass of carbon-14 is 1.3 times 10 to the minus 12 times the mass of carbon-12 and the mass of carbon-12 is 0.13 times the mass of the body and 0.13 times 1.3 times 10 to the minus 12 is 1.69 times 10 to the minus 13 times the mass of the body and we substitute that in for the mass of carbon-14 here and then we plug in as many numbers as we can, we can't substitute for the mass of the body though and that's fine. So we have 0.693 times 1.69 times 10 to the minus 13 and that's this number here times mass of the body, which I just moved to the end here multiplied by Avogadro's number divided by the half-life, which I left in units of years because we are going to end up multiplying by a year and so these units will be convenient actually so we are not going to convert this into seconds, as we might normally do. So we are dividing by 5730 years and then dividing by the molar mass, which I do a conversion to I am converting this into kilograms per mol because the units of the mass of the body are in kilograms and so for these units to work together, they both have to be in kilograms so I converted this into kilograms per mol. So this is 8.79007 times 10 to the 8 decays per year per kilogram multiplied by the mass of the body. So the energy produced then is this activity decays per year per kilogram times the mass of the body multiplied by time and I am looking up here now... we are substituting into this formula here we have just found out R so we have plugged in for R and that's all of this here multiplied by the time, which is 1 year and you can see now that these years cancel and then multiplied by the energy per decay and this is 1.05613 times 10 to the minus 5 joules per kilogram times the mass of the body. There! So now the efficiency then is 0.01 times 10 to the minus 3 joules per kilogram times the mass of the body— that's the energy absorbed here— divided by this energy produced that we just calculated here this works out to 0.947 that is the fraction of the decay energy that is absorbed.