Question
(a) A cancer patient is exposed to γ rays from a 5000-Ci transillumination unit for 32.0 s. The rays are collimated in such a manner that only 1.00% of them strike the patient. Of those, 20.0% are absorbed in a tumor having a mass of 1.50 kg. What is the dose in rem to the tumor, if the average energy per decay is 1.25 MeV? None of the s from the decay reach the patient. (b) Is the dose consistent with stated therapeutic doses?
Final Answer
- With a typical treatment protocol of up to 5 exposures, this dose will total 7.9 Sv which is almost the typical total dose for treatment of lung cancer.
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 19 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
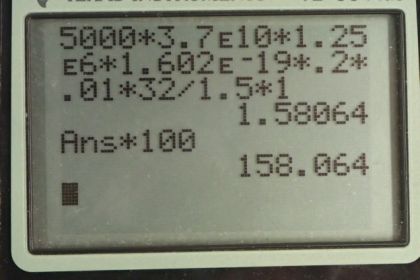
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Cobalt-60 is a radiation source producing gamma rays and 1 percent of the gamma rays from the cobalt-60 decay are directed towards the person's body. And of this 1 percent hitting the person's body, 20 percent of those gamma rays are hitting the tumor of the person's body or being absorbed by the tumor. So 20 percent of 1 percent of the total gamma ray radiation produced by the cobalt-60 is going into the tumor. This sample of cobalt-60 has an activity of 5000 curies and the exposure time is 32 seconds and the energy per gamma ray is 1.25 megaelectron volts and the total mass of the tumor is 1.50 kilograms and we are going to calculate the dosage in rems that's absorbed by this tumor. We also need to know the relative biological effectiveness of this type of radiation—gamma rays— and the answer to that is 1. So we find the absorbed dose in grays which is this part here not including the 1. As the absorbed dose in grays units of grays which is joules per kilogram and then we multiply that by the relative biological effectiveness to get an answer in sieverts and then we convert sieverts into rems. So let's go ahead and walk through where each of these numbers come from. So the dosage is the activity which is 5000 curies but we have to convert that into becquerels or in other words, decays per second; decays per second are more base unit version of becquerels and because this an mks unit so we multiply 5000 curies by 3.7 times 10 to the 10 and the curies cancel leaving us with decays per second And then we multiply by the energy per decay; we are told that's 1.25 megaelectron volts and the prefix mega means multiplied by 10 to the 6. So we have that many electron volts per decay. So we have a number of electrons per second now at this point in the equation and we want to know what the joules are so we convert electron volts into joules by multiplying by 1.602 times 10 to the minus 19 joules per electron volt and now we have joules per second absorbed well this is joules per second of total energy emitted by the cobalt only 1 percent of which hits the person and then 20 percent of that is absorbed by the tumor and so these two factors are accounting for the proportion that's absorbed by the tumor. And then this exposure happens for 32 seconds so now the seconds cancel. And we have joules but we want joules per kilogram in order to get units of grays and so we divide by the 1.5 kilogram mass of the tumor and then we multiply by the relative biological effectiveness of gamma rays which is 1 and we end up with 1.58064 sieverts. The question asks us to express our answer in rems so we multiply by 100 rems per sievert giving us dose equivalent of 158 rems. So is that typical of of radiotherapy for cancer? Well I guess how many exposures do they get there? Well this exposure in of itself is not enough to be a full radiotherapy; they would need both 5 exposures of this many sieverts each to reach 7.9 sieverts which is almost the low end of a typical dosage for lung cancer.