Question
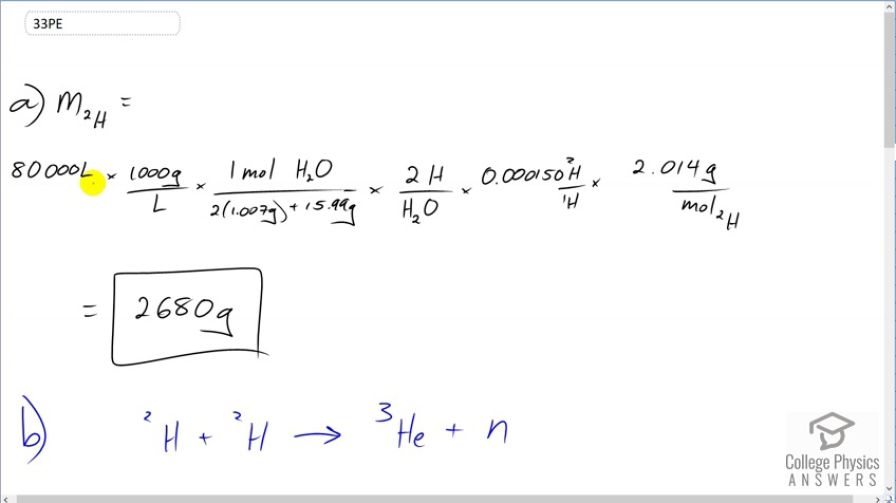
(a) Calculate the number of grams of deuterium in an 80,000-L swimming pool, given deuterium is 0.0150% of natural hydrogen.
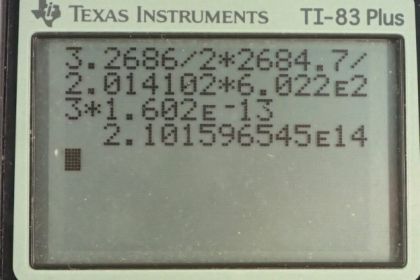
(b) Find the energy released in joules if this deuterium is fused via the reaction .
(c) Could the neutrons be used to create more energy?
(d) Discuss the amount of this type of energy in a swimming pool as compared to that in, say, a gallon of gasoline, also taking into consideration that water is far more abundant.
Final Answer
- Yes. For example,
- The energy released by fusion of deuterium in a swimming pool is times greater than that of a gallon of gasoline. Furthermore, there are many orders of magnitude greater mass of water on Earth than gasoline.
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 33 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In part (a) of this question, we are going to find the mass of deuterium in 80,000 liters of swimming pool water. So we'll turn this 80,000 liters into a mass by multiplying by 1000 grams for every liter—this is the density of water and then figure out how many mols this is by multiplying by 1 mol of water for every 2 times 1.007 grams—that's the molar mass of hydrogen plus 15.99 grams—molar mass of oxygen. And this molar mass is an average of you know the different isotopes, the deuterium and the tritium and so on. And then for every hydrogen or sorry every water molecule, there are 2 hydrogen atoms but I shouldn't say the word hydrogen because really we are talking about deuterium and so anyway there's 2 H's for every H 2 O and of those H's, 0.015 percent are deuterium and so this is 0.015 percent written as a decimal is going to be deuterium for every H and strictly speaking, there shouldn't be a 1 there, this is just H in general. OK So at this point we have the number of mols of deuterium then we multiply by 2.014 grams for every mol of deuterium and we get 2680 grams. So there's 2.7 kilograms or so or 2.68 kilograms of deuterium in a swimming pool that has a capacity of 80,000 liters. OK Then part (b) says suppose deuterium was made to react according to this reaction with a joined together to make a helium nuclide helium-3 plus a free neutron. So the amount of energy released for every pair of deuterium atoms or nuclei is going to be 2 times the mass of deuterium minus the mass of helium-3 minus the mass of a neutron times c squared. So we have 2 times 2.014102 atomic mass units for the deuterium atom and then minus the atomic mass of the helium atom minus the atomic mass of a bare neutron. And I can say the word atom which includes electrons because it turns out that there are two electrons included in this mass here because you know there's one electron in each deuterium atom times by 2 and so we have 2 electron masses included there and then we are subtracting away 2 electron masses included in this helium atom. And so what we are left with is the difference between the masses of the nuclei which is what we want. Okay and then we convert that into megaelectron volts per c squared and then multiply by c squared and we end up with 3.2686 megaelectron volts of energy released for every pair of deuterium nuclei. Then we'll figure out, you know, how much total energy will be released by if you were to react all of the deuterium nuclei present in the swimming pool. And so we have this much energy for every pair of deuterium nuclei. And so the arithmetic we are doing here is 3.2686 divided by 2 because we want the energy per pair and then multiply it by this many grams of deuterium in swimming pool times by 1 mol for every 2.014102 grams of deuterium times by the number of atoms per mol and then times by the number of joules per megaelectron volt and we are gonna end up with after all these units cancel out here that we are going to end up with the number of joules and this isn't really a unit. So or you can think of it as a unit you could say this is atoms of H 2 and then it would cancel. OK So we are left with joules and that is 2.10 times 10 to the 14 joules of energy could be released if you were able to fuse all the deuterium atoms in a 80,000 liter swimming pool. Part (c) would the neutron that's released be usable to release further energy and the answer is yes. It could for example impact a hydrogen nucleus and create deuterium and a gamma ray and thereby release energy. Then in part (d), we'll compare the energy released by fusing this deuterium in the swimming pool with the energy release by burning gasoline. And so in table 7.1, we find that one gallon of gasoline can release 1.2 times 10 to the 8 joules of energy and we have this 2.1 times 10 to the 14 joules of energy released by the deuterium in the swimming pool divided by the energy from a gallon of gas and they are different by a factor of 2 times 10 to the 6. And now granted we have a few orders of magnitude greater volume of water in the swimming pool—80,000 liters versus only 1 gallon of gasoline— but nevertheless you know, there's many orders of magnitude greater amount of energy released in the deuterium fusing and furthermore, there's a hugely greater amount of water in the world than there's gasoline so we can say that there's much more energy available from fusing deuterium and water than there is from gasoline in the world.