Question
An expensive vacuum system can achieve a pressure as low as at . How many atoms are there in a cubic centimeter at this pressure and temperature?
Final Answer
Solution video
OpenStax College Physics, Chapter 13, Problem 31 (Problems & Exercises)
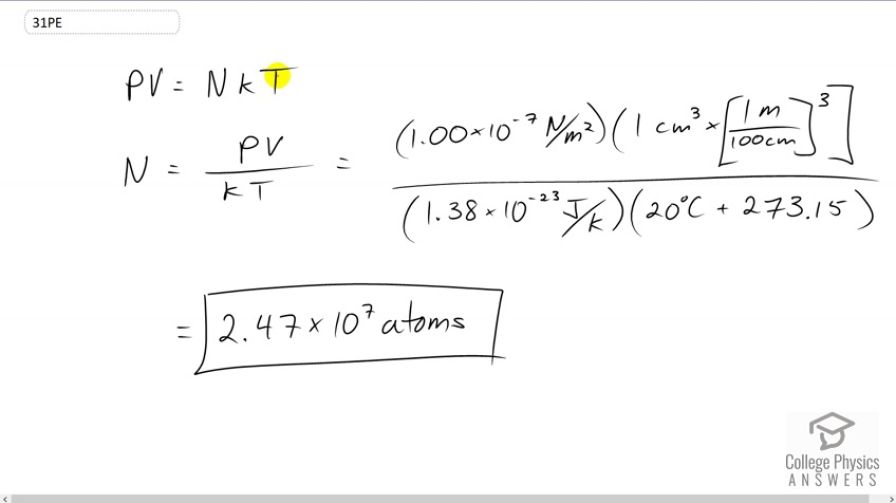
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the number of atoms in a cubic centimeter inside this vacuum. So we're given the pressure, the volume, and the temperature and we know that pressure times volume equals the number of atoms times Boltzmann's constant, times the temperature written in absolute temperature as Kelvin. So we divide both sides by k T to solve for N. So the number of atoms is pressure times volume divided by Boltzmann's constant times temperature. So it's one times ten to the minus seven newtons per square meter, times one cubic centimeter but we have to convert that into cubic meters in order to correspond to these units that are here. So we have one cubic centimeter times one meter for every 100 centimeters three times, and then we're going to divide by Boltzmann's constant, 1.38 times ten to the minus twenty-three joules per Kelvin and then times by the temperature converted into Kelvin by adding 273.15 to the 20 degrees Celsius. This makes 2.47 times ten to the seven atoms.
