Question
What is the ratio of the velocity of a particle to that of an particle, if they have the same nonrelativistic kinetic energy?
Final Answer
85.4
Solution video
OpenStax College Physics, Chapter 31, Problem 11 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
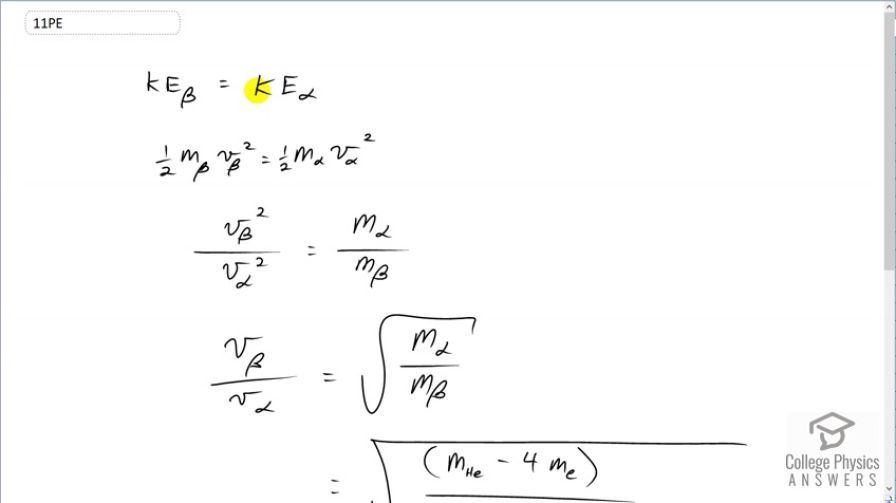
This is College Physics Answers with Shaun Dychko. We are going to find the ratio of velocities of a β-particle to an α-particle given that they have the same kinetic energies and non-relativistic speeds. So we have one-half times mass of a β-particle times its speed squared equals one-half times mass of the α-particle times its speed squared. And we can multiply both sides by 2 and also divide both sides by v α squared and m β and we end up with these canceling here and the 2's cancel and then on this side, the masses cancel and we are left with v β squared over v α squared on one side and then on the other side, we have mass α divided by mass β. And then we'll take the square root of both sides and now this is then the ratio of the speeds. And then we can substitute in for these things here. So the mass of the α-particle will be the mass of a helium atom and when you say the word atom, you are including electrons in the atom and we don't want to include the mass of the electrons. So but our data table nevertheless includes those electrons and so we have to subtract their mass away; that's why there is a minus 4 times mass of the four electrons that are included in the atomic mass data table in appendix A. So we have then this difference then in the numerator is the mass of a helium nucleus. So that mass gets divided by the mass of a β-particle which is an electron; they didn't know that it should be called an electron when they first discovered that particle and so we have 4.002603 atomic mass units for a helium atom minus 4 times 5.4858 times 10 to the minus 4 atomic mass units for an electron divided by the mass of an electron and this gives 85.4. So the speed of an electron in would be 85.4 times that of an α-particle if they have the same kinetic energy.
