Question
Armor-piercing shells with depleted uranium cores are fired by aircraft at tanks. (The high density of the uranium makes them effective.) The uranium is called depleted because it has had its removed for reactor use and is nearly pure . Depleted uranium has been erroneously called non-radioactive. To demonstrate that this is wrong: (a) Calculate the activity of 60.0 g of pure . (b) Calculate
the activity of 60.0 g of natural uranium, neglecting the and all daughter nuclides.
Final Answer
Solution video
OpenStax College Physics, Chapter 31, Problem 61 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
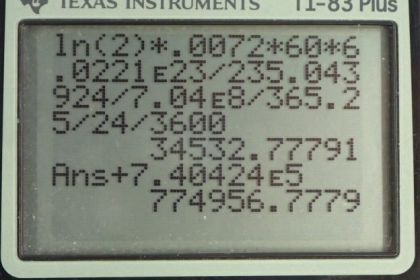
This is College Physics Answers with Shaun Dychko. We are going to calculate the activity of uranium-238 which is pure of only that isotope and then we'll compare that with the activity of a natural sample of the uranium which has both the 238 and the 235 isotopes in it and we'll see that the radioactivies are pretty much the same. So let's first collect a whole bunch of data together here; we have the half-life of uranium-238 and the half-life of uranium-235; the total mass is 60 grams in these well, we're just told to consider a sample of 60 grams here and here's the molar mass of uranium-238 and uranium-235 and all this data comes from appendix A. So part (a)—pure uranium-238— what's the activity of a 60 gram sample? So the activity is logarithm of 2 times the number of atoms divided by the half-life and we are going to express the number of atoms in terms of mass because we are told that the mass is 60 grams and so we divide the 60 grams by the molar mass times by Avogadro's number and get the number of atoms and then we substite that in for n and you can check the units here and see it's grams divided by grams per mol times by number of atoms per mol and this works out to number of atoms. OK. So the activity is log 2 times mass times Avogadro's number divided by molar mass times half-life. And so for this pure uranium-238 sample, we have log 2 times 60 grams times Avogadro's number divided by the molar mass of uranium-238 times the half-life expressed in seconds and this gives 7.46 times 10 to the 5 becquerels. So it's still radioactive even though it is depleted so to speak meaning that its had the uranium-235 removed for nuclear reactor and heaven forbid, nuclear weapons use. In part (b), we are going to figure out the activity of a natural sample of uranium which has both these isotopes. Now, the activity will be the sum of the activities of the respective isotopes and to get the activity of the uranium-238, we can take the activity calculator in part (a) and multiply it by the relative abundance of uranium-238 which is 99.2745 percent that I have written here as a decimal. This works out to 7.40424 times 10 to the 5 becquerels. And then the activity of the uranium-235 isotope in this mixture is gonna be natural log of 2 times its relative abundance of 0.00720 times 60 grams times Avogadro's number divided by the molar mass of uranium-235 times the half-life of uranium-235, written in seconds, and this works out to 3.4532 times 10 to the 4 becquerels. So we add these two activities together here and get a total activity of 7.75 times 10 to the 5 becquerels and that's nearly the same as 7.46 times 10 to the 5 becquerels and so we can definitely say that if you consider natural uranium to be radioactive, depleted uranium certainly also is radioactive.