Question
The purpose of this problem is to show in three ways that the binding energy of the electron in a hydrogen atom is negligible compared with the masses of the proton and electron. (a) Calculate the mass equivalent in u of the 13.6-eV binding energy of an electron in a hydrogen atom, and compare this with the mass of the hydrogen atom obtained from Appendix A. (b) Subtract the mass of the proton given in Table 31.2 from the mass of the hydrogen atom given in Appendix A. You will find the difference is equal to the electron’s mass to three digits, implying the binding energy is small in comparison. (c) Take the ratio of the binding energy of the electron (13.6 eV) to the energy equivalent of the electron’s mass (0.511 MeV). (d) Discuss how your answers confirm the stated purpose of this problem.
Final Answer
- The difference is nearly the rest mass of a free electron, to four significant figures.
- Part (a) shows that the electron binding energy () is negligible compared to the combined mass of a proton and electron. Part (b) shows that the difference in mass between a hydrogen atom and a proton is essentially the mass of an unbound electron, which indicates that the electron binding energy didn't really affect the bound electron mass in the atom. Part (c) directly compares to and shows that is smaller by 5 orders of magnitude.
Solution video
OpenStax College Physics, Chapter 31, Problem 75 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
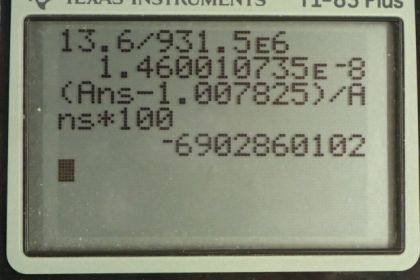
This is College Physics Answers with Shaun Dychko. In part (a), we compare the binding energy of an electron to the mass of a hydrogen atom. So converting this 13.6 electron volts— binding energy of an electron— into atomic mass unit equivalents, we multiply by 1 atomic mass unit for every 931.5 times 10 to the 6 electron volts giving us 1.46 times 10 to the minus 8 atomic mass units. So we'll find the percent difference between these two and so we'll take this binding energy, expressed in atomic mass units, minus the mass of a hydrogen atom and divide by the binding energy times by 100 percent and we get that the binding energy is 6.9 billion percent less than the mass of a hydrogen atom. So this binding energy of an electron is very small compared to the mass of a hydrogen atom. In part (b), we take the difference between mass of a hydrogen atom and the mass of a bare proton and that's 1.007825 atomic mass units minus 1.007276 atomic mass units giving 0.000549 atomic mass units. So this is the difference between the two and this essentially is the mass of a bare electron and because that's the case, it means that this binding energy of the electron didn't change its mass very much. When a sub-atomic particle is bound into some system, it loses some of its mass. But what we are seeing here though is that this mass difference between a hydrogen atom and a bare proton equals the rest mass of a bare electron meaning its mass when it's contained in this bound hydrogen atom hasn't changed much as a result of that binding energy suggesting that the binding energy is very small. Then in part (c), we compare the binding energy of the electron directly with the electron's rest mass and this works out to 2.7 times 10 to the minus 5 is the ratio. So the binding energy of the electron is 5 orders magnitude less than the rest mass of the electron. And part (d) basically kinda says what I already said while I went through each part but part (a) shows that the electron binding energy is negligible compared to the combined mass of a proton and electron that is compared to a hydrogen atom in other words. Part (b) shows that the difference in mass between a hydrogen atom and a proton is essentially the mass of an unbound electron which indicates that the binding energy didn't change the mass of a bound electron in the atom. So the binding energy is small, in other words. And part (c) directly compares binding energy of an electron to its rest mass and shows that it's small by 5 orders of magnitude.