Question
Natural uranium is 0.7200% and 99.27% . What were the percentages of and in natural uranium when Earth formed years ago?
Final Answer
Note: at 0:10 I mention the percentage of Uranium-238 as 99.2748%, but it's corrected in the closed captions (and in the written text) as 99.2745%.
Solution video
OpenStax College Physics, Chapter 31, Problem 57 (Problems & Exercises)
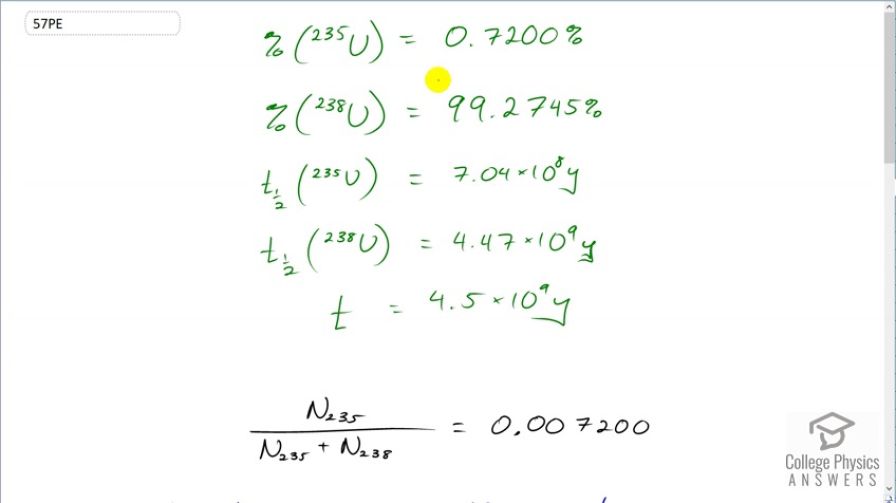
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We know what the relative abundance of the uranium-235 and uranium-238 isotopes are in the present day Earth. uranium-238 comprises 99.2745 percent of a sample of uranium where as 235 isotope comprises of 0.72 percent of a sample and the question is what were the percentages when the Earth was first formed four and a half billion years ago? And the percentages will be different because the half-lives are different for these materials and uranium-235 decays in order of magnitude faster than uranium-238 and so we should expect a higher percentage of uranium-235 when the Earth was first formed. OK. So we know that uranium-235 divided by the number of uranium-235 plus the uranium-238 currently equals 0.007200 and to help us answer this question, we are going to hypothetically suppose that there's a total number of uranium atoms of 10000 atoms in which case, currently there would be 72 atoms that are of isotope 235 that is 0.007200 times 10000 makes 72 and whereas the uranium-238 would be 9927 atoms. So we are going to use this formula to figure out the original number of uranium-235 atoms given the present day number of 72. And then we'll also find the original number of uranium-238 atoms and then we'll find the ratio that existed originally. So we substitute for the decay constant with natural logarithm divided by half-life and so by the way to divide when you divide by e to the negative λt, you can instead of dividing by e to the negative λt, you can write this as multiplying by e to the positive λt which is what we have here. And so N naught equals the present number of atoms—N— times e to the positive λt. So we substitute for λ here and this is for uranium-235, the original number, equals the present number 72 times e to the natural logarithm of 2 divided by the half-life of uranium-235 times the amount of time that has passed since the Earth was formed and this makes 6046.9 atoms in our hypothetical sample of that we started here with of 10000. So in order to have 72 now of uranium-235, we must have started with 6046.9; well except this 0.9 for now, this is just a calculation I mean of course you can't have less than 1 atom. OK. And the original number of uranium-238 would be 9927 present day times either the natural logarithm of 2 divided by the half-life of uranium-238 multiplied by the age of the Earth and that makes 19946.6. atoms. So the percentage of uranium-235 originally is going to be the number that we would have started with divided by the total number of atoms which is 23 percent and for uranium-238, it's the same type of calculation giving us 77 percent. So this would have been the relative abundance of the two isotopes when the Earth was first formed.


