Question
Show that the activity of the in 1.00 g of found in living tissue is 0.250 Bq.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 31, Problem 47 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
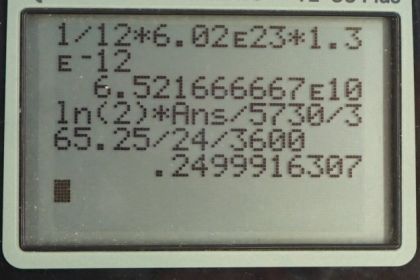
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have 1 gram of living tissue and the fact that it says living tissue the fact that it's living is an important detail because it means the ratio of carbon-14 to carbon-12 isotopes in the carbon in this living tissue will be the same as found in the air in the atmosphere. After the tissue dies, there's no longer any uptake of carbon from the atmosphere because the tissue is no longer alive and then the carbon-14 begins to decay and then the ratio of carbon-14 and carbon-12 changes with time and this is the principal upon which carbon dating is based. So looking at the activity of an old sample of tissue, and extrapolate what the age of it is based on how much carbon-14 is left. OK. But in living tissue, we expect the ratio of carbon-14 to carbon-12 to be 1.3 times 10 to the minus 12; we got that from example [31.5]. The half-life of carbon-14 is 5730 years; I found that in appendix B and we are gonna show that the activity is 0.250 becquerels. So the activity is logarithm of 2 times the number of carbon-14 atoms divided by the half-life of carbon-14. So the number of atoms is the number of grams of tissue which is 1 gram times the number of mols for every 12 grams; this is the molar mass of the tissue, which we take to be, you know, the molar mass of carbon-12 because carbon-14 makes such a small fraction of the sample its extra mass doesn't really change the average of this full sample. So to as many significant figures as we are concerned with, this tissue has a molar mass of 12 grams per mol but we write 12 grams per mol in a reciprocal form as 1 mol for every 12 grams so that these grams cancel leaving us with number of mols which we can then convert into the number of atoms by multiplying by Avogadro's number. So we multiply by 6.02 times 10 to the 23 atoms for every mol and then that's the total number of carbon atoms and then multiply that by the fraction of those which are carbon-14 atoms—1.3 times 10 to the minus 12— and we get the number of carbon-14 atoms 6.5217 times 10 to the 10 atoms. Then we take this number of carbon-14 atoms multiply by logarithm of 2 and divide by the half-life expressed in seconds in order to get our answer in becquerel's. So we are taking this half-life in years times the number of days per year times number of hours per day times the number of seconds per hour and we end up with 0.250 becquerel's as we expected.