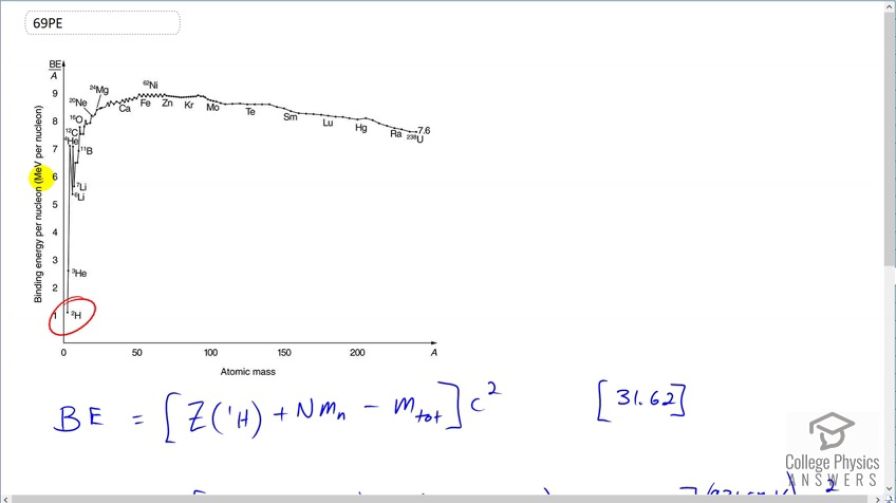
${}^2\text{H}$ is a loosely bound isotope of hydrogen. Called deuterium or heavy hydrogen, it is stable but relatively rare—it is 0.015% of natural hydrogen. Note that deuterium has Z = N , which should tend to make it more tightly bound, but both are odd numbers. Calculate BE/A , the binding energy per nucleon, for ${}^{2}H$ and compare it with the approximate value obtained from the graph in Figure 31.27.

Video Transcript

This is College Physics Answers with Shaun Dychko. We are going to calculate the binding energy per nucleon of deuterium; this is a graph of binding energy per nucleon and megaelectron volts per nucleon. So deuterium has 2 nucleons so that's why this denominator is 2 here— this is the mass number in the denominator— and the binding energy is you find the mass energy of however many protons there are in the atom or nucleus; when I say atom, we are going to be using atomic masses here that we look up in appendix A and those atomic masses include the mass of the attached electrons because atoms have electrons, nuclides do not have electrons, a nuclide is just a bare nucleus. Now this mass of these electrons does not concern us though because we are going to be subtracting the atomic mass of the atom here which includes the same number of electrons and so we are having electrons that we don't want in this number and then we are gonna be taking that same number of electrons away included in this number. OK. So we have 1 proton in the deuterium nucleus and so we have 1 multiplied by the atomic mass for hydrogen plus 1 neutron and then minus the atomic mass for deuterium. And then we convert this into megaelectron volts per c squared for every atomic mass unit and multiply by c squared, divide this by 2 and we end up with 1.112 megaelectron volts per nucleon. And this matches what's shown in figure 31.27; this is 1.11 or so.