Question
Large amounts of depleted uranium () are available as a by-product of uranium processing for reactor fuel and weapons. Uranium is very dense and makes good counter weights for aircraft. Suppose you have a 4000-kg block of . (a) Find its activity. (b) How many calories per day are generated by thermalization of the decay energy? (c) Do you think you could detect this as heat? Explain.
Final Answer
- . This would probably not be noticeable.
Solution video
OpenStax College Physics, Chapter 31, Problem 63 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
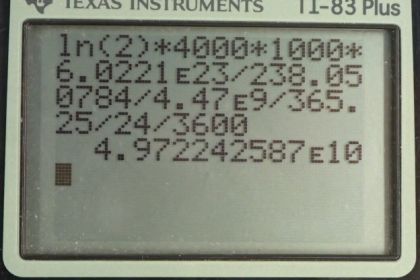
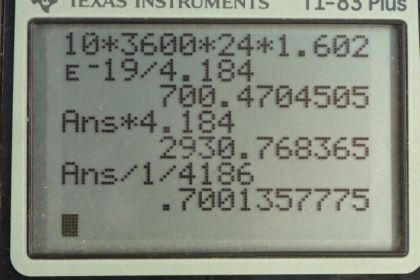
This is College Physics Answers with Shaun Dychko. Suppose we have 4000 kilograms of pure uranium-238. We are asked in part (a) to figure out its activity. So we need to know what its half-life is which we look up in appendix A— 4.47 billion years— and its molar mass will be needed to convert this kilograms into the number of uranium atoms. So the activity of nuclide is natural logarithm of 2 times the number of nuclei divided by the half-life. Now we can substitute for the number of nuclei in terms of mass because mass is what we are given and so we have mass divided by molar mass multiplied by Avogadro's number which gives the number of atoms and you can check the units to confirm that this formula works here. So we have grams in our mass divided by grams per mol in our molar mass and then multiply by the number of atoms per mol which is Avogadro's number. And the grams cancel, these reciprocal mols in the denominator cancel with the reciprocal mols here and we are left with number of atoms. So we substitute all of this in place of capital N. So the activity is logarithm of 2 times the mass times Avogadro's number divided by the molar mass times the half-life. So we have logarithm of 2 times 4000 kilograms converted into grams which is kind of unusual; normally, we have meters, kilograms and seconds in our formulae but today we are going to have grams instead of kilograms. And the reason we do that is because our molar mass for the uranium-238 isotope is expressed in units of grams per mol so we want these grams to match in the top and the bottom and cancel. Then we multiply this top here by Avogadro's number divide by the molar mass multiply by the half-life, expressed in units of seconds, and we get 4.97 times 10 to the 10 becquerels is the activity of 4000 kilograms of uranium-238. And this question in part (b) says how many calories per day if you were to turn all of that decay energy into heat, how many heat calories would be produced per day? So the appendix B tells us what the decay energy is and 77 percent of the time, the decay energy is 4.27 megaelectron volts and 23 percent of the time, it is 4.22 megelectron volts and so we take the weighted average of these two to get 4.2585 megaelectron volts on average per decay. So that energy gets multiplied by the number of decays per second which is what becquerels is in base units and that gives us the number of electron volts per second and then we have to convert the seconds into days by multiplying by 3600 seconds per hour times by 24 hours per day and then we have at this point, electron volts per day which we then convert into joules and then we have a conversion factor from joules to calories. So 1 calorie for every 4.184 joules and we end up with 700 calories per day. Then question (c) says would this thermal energy be noticeable? Well we can use this formula for the amount of heat that will raise the temperature of a material by a certain amount and figure out what will the temperature change be if we assume that we have 1 kilogram of water, say. And so we divide both sides by mc and so we have the change in temperature is the heat energy divided by mc. So that's 700 kilograms, or calories, per day, I should say times 4.184 joules per calorie and divide that by kilogram and then multiply by the specific heat of water—4186 joules per kilogram per Celsius degree— giving a temperature change of 0.7 Celsius degrees if you had 1 kilogram of water absorbing all that heat energy from the uranium-238 decay. This would probably not be noticeable.