Question
(a) Calculate the energy released in the decay of (b) What fraction of the mass of a single is destroyed in the decay? The mass of is 234.043593 u. (c) Although the fractional mass loss is large for a single nucleus, it is difficult to observe for an entire macroscopic sample of uranium. Why is this?
Final Answer
- The uranium decays so slowly that very little decays, so the mass change is unnoticeable on a human time scale.
Solution video
OpenStax College Physics, Chapter 31, Problem 41 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
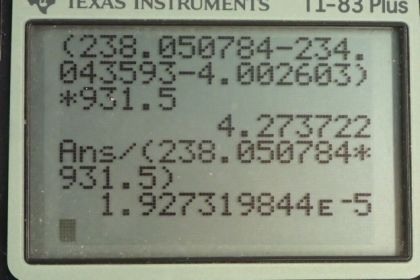
This is College Physics Answers with Shaun Dychko. We are going to calculate the energy released during α-decay of uranium-238 into thorium-234. So the energy released will be the change in mass times c squared; that's equation 16 from chapter 31. And so we have the atomic mass of uranium— 238.050784 atomic mass units— minus the atomic mass of thorium minus the atomic mass of helium and we don't know need to worry about mass electrons here because we have an electron mass for 92 electrons including in the atomic mass of uranium. And then we have 90 electron masses included in the atomic mass for thorium plus 2 electron masses included in the atomic mass of helium. So the electron masses are canceling out; we have 92 included among the products and then 92 among the reactant. OK. So this difference times c squared after converting into megaelectron volts per c squared is 4.273 megaelectron volts. And the question in part (b) asks what fraction of mass is lost during this decay? So we wanna find the change in mass divided by the mass that we started with. So the change in mass is this many megaelectron volts per c squared and then divide that by the mass that we started with converted into units of megaelectron volts per c squared and this is 1.927 times 10 to the minus 5. Now in part (c) we are asked to figure out, you know, seeing as some mass is disappearing during the decay of uranium-238, how come we don't really measure that in a macroscopic sample of uranium-238? And the reason for that is that the half-life is so long this half-life is the age of the planet Earth basically. And so it decays so slowly that you can observe very little or non-negligible or sorry negligible I should say mass change in a sample because the sample is decaying so slowly.