Question
Natural uranium is 0.7200% , 99.27% , and 0.0055% . (a) What were the percentages of , , and in natural uranium when Earth formed years ago? (b) What is unreasonable about this result? (c) What assumption is responsible? (d) Where does come from if it is not primordial?
Final Answer
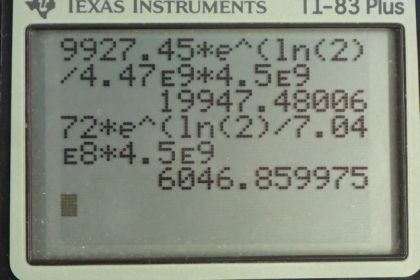
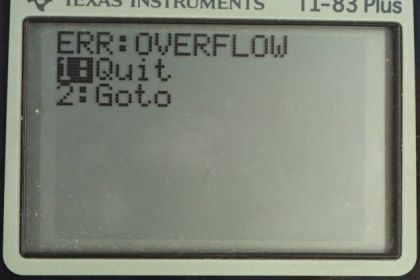
- The calculator can't compute such a large number.
- This calculation would suggest an amount of that exceeds all the ordinary matter in the universe.
- The assumption that a primordial initial quantity of existed, and has since decayed and not been produced, is false.
- is continually produced by radioactive decay.
Solution video
OpenStax College Physics, Chapter 31, Problem 67 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to calculate what the relative abundance is of the three different isotopes of uranium in the priomordial Earth when it was first created. And so we are going to assume that we have 10000 atoms of uranium today and 99.2745 percent of those are going to be uranium-238 and so that would make it 9927.45 atoms of this isotope. 0.72 percent written as a decimal is 0.00720 our uranium-235 which is 72 atoms and then given this 0.0055 percent written as a decimal here for the uranium-234 isotope show up as 0.55 atoms today. And so we are making an assumption that this isotope existed when the Earth was first formed and has since been decaying and not produced on during the time since the Earth was made and has now reached an abundance of 0.55 atoms for every 10000. OK. And here are the half-lives of these different isotopes and the amount of time that has passed since the Earth was formed is four and a half billion years. So we have this formula to tell us the number of atoms today given a initial number times e to the negative decay constant times t; this is equation 36 from chapter 31 and then we can divide both sides by e to the λt or divide by e to the negative λt I should say which works out to e to the positive λt on the other side so we have N naught equals N times e to the positive λt. λ is a decay constant which we can substitute with natural logarithm of 2 divided by half-life so we do that substitution here. And so here we have a formula for the initial number of atoms given a present number of atoms and the amount of time that has passed and the half-life of that isotope. So we do this calculation three times for each of the three isotopes. So the number of uranium-238 atoms is 9927.45 today times e to the natural log of 2 divided by the half-life of uranium-238 times the age of the Earth which is 19947.5 atoms. And the same kind of calculation for uranium-235 giving 6048 atoms and now when you do this with uranium-234 however, you get an error on the calculator because this exponent is so large the calculator can't even do this calculation. And the reason for this is that while we have made an incorrect assumption this uranium-234 is not something that was plunked down on to the Earth when it was formed has slowly decayed since; that assumption is true for uranium-238 and uranium-235; uranium-234, on the other hand, is being created slowly as a part of the decay process. So here's the decay chain for uranium-238 it does α-decay to thorium which then does β-decay to protactinium which then does β-decay to uranium and then here we have uranium-234 which appears as part of this decay chain. Oh also this is not palladium, this is protactinium. Yeah, okay. So this calculation is unreasonable because of course the calculator can't even do it and if you had as many atoms as this calculation would show, it would have a mass greater than that of the universe and if I guess I'm just doing some assumptions here if you look at Wikipedia, you have 4.5 times 10 to the 51 kilograms of all ordinary matter in the universe that is non-dark matter and if all mass was uranium-234 then the number of atoms would be well here's the mass of the universe in grams divided by this many grams per mol for uranium times this Avogadro's number, it would be 1.2 times 10 to the 76 atoms. And even that is a number that's less than all of this which is the calculation here. So if you make the clearly absurd assumption that every single atom in the universe is a uranium-234 atom even then you would still not have a number as big as this. OK. So uranium-243 is not primordial. And there we go; it's been continuously produced by this radioactive decay of uranium, uranium-238 that is.