Question
(a) What is the intensity in watts per meter squared of a just barely audible 200-Hz sound? (b) What is the intensity in watts per meter squared of a barely audible 4000-Hz sound?
Final Answer
Solution video
OpenStax College Physics, Chapter 17, Problem 67 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
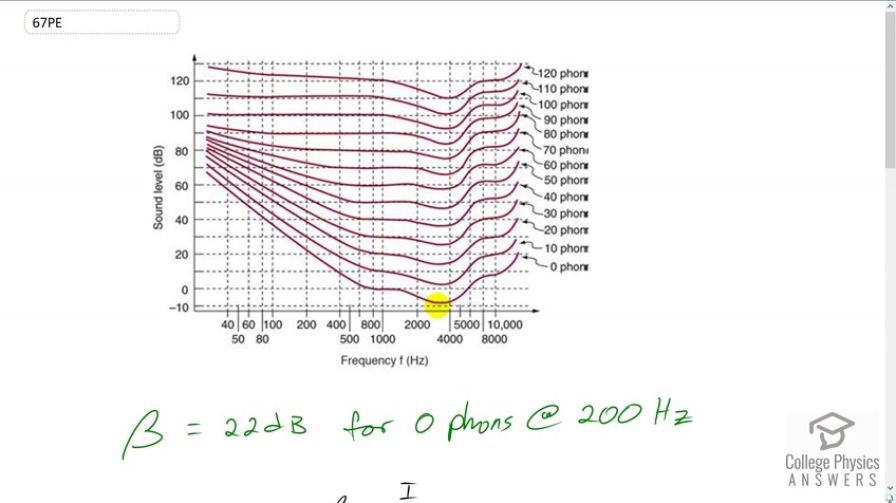
This is College Physics Answers with Shaun Dychko. If something is barely audible that means it has a perceived loudness of zero phons and so at a frequency of 200 hertz, we can move up this graph until we encounter this zero phons line, which I’ll highlight the bottom one and we read off what its sound level is in decibels, its about 22 or so and then the rest of our work in question is to figure out what sound intensity, and I mean sound intensity not sound intensity level. What sound intensity correspond to 22 decibels. So, we need to know what, how to solve this for I. So, this is the formula for decibels sound intensity level is ten times logarithm of intensity in watt per square meter divided by reference intensity which is the threshold of hearing at either 1000 hertz or 4000 hertz, I figure which one is this, I think its 1000 hertz, yeah. So, yeah it has to be 1000 hertz because there is zero decibels at 1000 hertz, anyway that’s in a side. So, lets get rid of it to solve for I. So, we can divide both sides by ten, switch the sides around and we have logarithm of intensity over reference intensity is the sound level divided by ten and then make both sides exponent of ten and on the left side, ten to the power of logarithm base ten is going to be the argument of logarithm. So, I over I naught and that equals ten to the power of sound level over ten and then we can solve for I by multiplying both sides by I naught. So, intensity is reference intensity times ten to the power of beta over ten and so we have a 22 decibels is the sound level for barely perceptible sound of frequency 200 hertz. So, we have ten to the minus twelve watt per square meter, that’s the reference intensity time ten to the power of 22 decibels over ten gives 1.58 times ten to the minus ten watt per square meter and then next part of the question asks for the intensity at 4000 hertz. So, we look at 4000 on this x-axis and go up to the point where it intersects the zero phons line and find out what is the y-value there, looks like it about negative eight and so we can plug in negative eight into this formula. So, we have intensity of ten to the minus twelve watt per square meter times ten to the power of negative eight decibels over ten which give 1.58 times ten to the minus thirteen watt per square meter and so we can see these three orders of magnitude difference in intensity, just as a result of changing frequency. Both of these sounds are equally barely audible, but their different frequencies require different intensities to be just barely audible.
