Question
(a) A bat uses ultrasound to find its way among trees. If this bat can detect echoes 1.00 ms apart, what minimum distance between objects can it detect? (b) Could this distance explain the difficulty that bats have finding an open door when they accidentally get into a house?
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 0.172 m0.172 \textrm{ m}
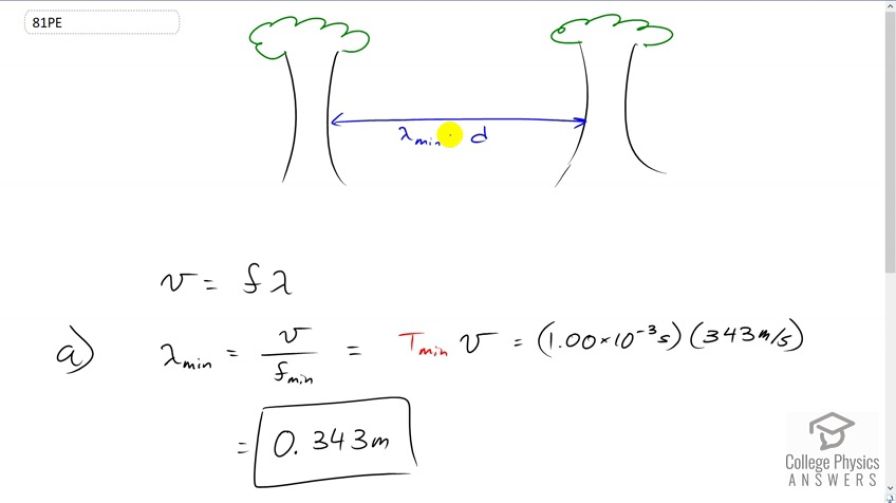
  2. Since doors are wider than 17 cm, this does not explain why bats have a difficult time finding the door to exit a house.

Note: The video needs to be re-done. The final answer written above is correct, and so is the calculator screenshot, but the video made the incorrect assumption that resolution was limited to the wavelength, as it is approximately when using a microscope, for example.

Solution video

OpenStax College Physics, Chapter 17, Problem 81 (Problems & Exercises)

OpenStax College Physics, Chapter 17, Problem 81 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 17, Problem 81 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. The minimum distance between points that can be observed with the wave are approximately equal to the wavelength, this is approximately equal to. So, for this bat, using ultrasound to measure the distance between two trees or distance between, yeah, two trees in this question, we know that this has to be true. So, using the wave speed formula, and we're given the minimum time resolution of the bat's perception. The minimum amount of time between receiving two different echoes. And, we'll substitute that for frequency because we're going to find out what this minimum wavelength is by dividing both sides by F here. And, it's going to be the wave speed divided by the minimum frequency. And, we'll say that the frequency is one over period. And so, we'll substitute period in place of one over frequency. And that's what we've done here. And so, the bat's minimum time that it can perceive is one millisecond, which is one times ten to the minus three seconds, and we multiply that by the speed of sound in air, which is 343 meters per second, which gives a minimum spatial resolution of 0.343 meters. Since doorways are wider than 34 centimeters, this spatial resolution cannot explain why bats have a difficult time finding the door to exit a house.

Comments

Submitted by ts on Thu, 02/18/2021 - 09:28

link

Hello,

I am wondering why the answer is not divided by 2 in this problem since it is an echo that bounces back to the source. In a previous solution for this chapter (#9 I believe) the question has nearly identical wording and structure, but in that problem the solution is divided by two to account for the fact that the sound wave is reflected. I have copied the problem here for convenience: 9. (a) If a submarine’s sonar can measure echo times with a precision of 0.0100 s, what is the smallest difference in distances it can detect? (Assume that the submarine is in the ocean, not in fresh water.)

That solution involves using the equation 2d=Vwt2d = Vwt to solve for d, however if I use that same method for this problem I get an answer that is 1/2x the correct value. Is there something I am missing in the wording of these two questions?

Thanks!

Hello ts,
Thank you so much for this question. You've uncovered an error! The answer should be divided by 2, as you suggested. I was working with a different (and incorrect) point of view where the resolution was approximately limited to the wavelength, as it is with a microscope. From p. 1312 in chapter 29, the text says "Resolution, or observable detail, is limited to about one wavelength.", but that doesn't really apply here since the bat is using a linear back-and-forth echolocation, not a diffraction limited scenario of a wave passing through an aperture (the door, from this perspective).
I have corrected the final answer and updated the calculator screenshot. I'll replace the video after I've completed all of the remaining even numbered solutions.
All the best,
Shaun