Question
(a) If a submarine’s sonar can measure echo times with a precision of 0.0100 s, what is the smallest difference in distances it can detect? (Assume that the submarine is in the ocean, not in fresh water.)
Final Answer
- Spatial resolution is . Shape features of size less than that will not be detected. Object smaller than will not be noticed.
Solution video
OpenStax College Physics, Chapter 17, Problem 9 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
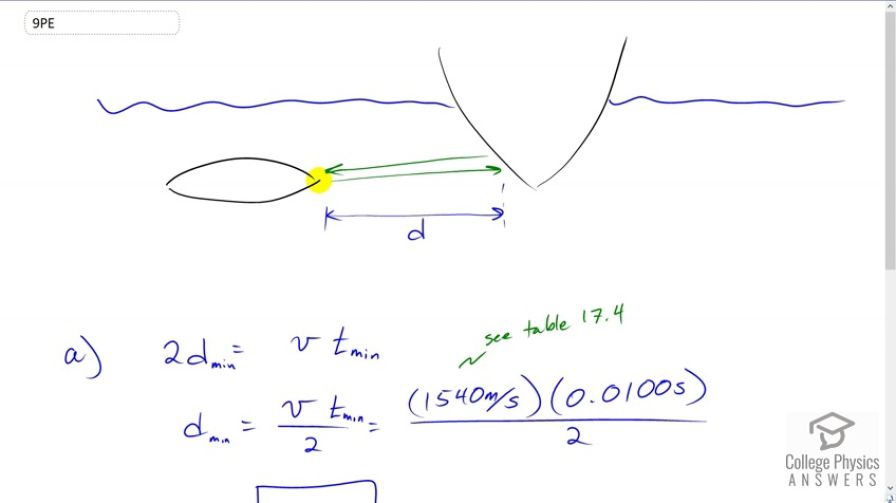
This is College Physics Answers with Shaun Dychko. The submarine has a certain time resolution in the electronics of its sonar. And what that means is that when it is measuring an echo which is sound that has bounced off some other object in returned. This is the echo that come back from hitting this boat. That echo has to return in the time greater than 0.01 seconds. If it returns any quicker than that, then the sonar will not be able to measure that echo. We will not notice it. And so I am going to answer two questions here. The question being asked is: what is the minimum difference in distance that can be measured. And what I am going to first answer is: what is the minimum distance in total that can be measured? So, how close can the submarine get to the boat and perceive that it just there? If the submarine is too close to the boat, the sonar will not notice the boat, because the echo will return so quickly that it will not be able to measure that echo. So, when the sound leaves the submarine, it travels the distance d separating the submarine from the boat. This is d minimum, we will assume. And then it bounces off the boat and return to the submarine. And so the sound has traveled two times this minimum distance from the boat. And that distance, the total distance two times the minimum distance is going to be the speed of sound multiplied by this minimum time that the electronics can measure. So, we will divide both sides by two here. And we get the minimum distance then is speed of sound multiplied by the minimum time divided by two. Now the speed of sound in salt water is 1540 meters per second which I looked up in table 17.4 and multiply that by the minimum time resolution of the electronics which is 0.01 seconds and divided by two giving us 7.70 meters. So, this submarine has to be 7.7 meters or more away from the boat in order to see it which is a little bit counter-intuitive. Normally, you think that getting closer to something makes it easier to see things. And that is true for your eyes. But with sonar it is working differently. If you get too close to an object, the sonar equipment will not notice that it is there because the echo will return too quickly for the electronics to process it. So, this means the spatial resolution of this equipment is 7.7 meters. And so if an object has a shape like this curvature of a boat, the sonar will be able to perceive the curvature of boat only if maybe the bottom tip and this part here has to be separated by more than 7.70 meters. If these positions are closer to each other than 7.7 meters, then the sonar will not be able to notice that they are different distances. So the sonar is not very good at resolving shapes and shape features have to be, have to have more than 7.7 in order to see them. So shape features that are less than 7.7 meters will not be detected. And also objects that are smaller than 7.7 meters will not be noticed by this sonar equipment.
