Question
By what fraction will the frequencies produced by a wind
instrument change when air temperature goes from to ? That is, find the ratio of the frequencies at those temperatures.
Final Answer
Solution video
OpenStax College Physics, Chapter 17, Problem 49 (Problems & Exercises)
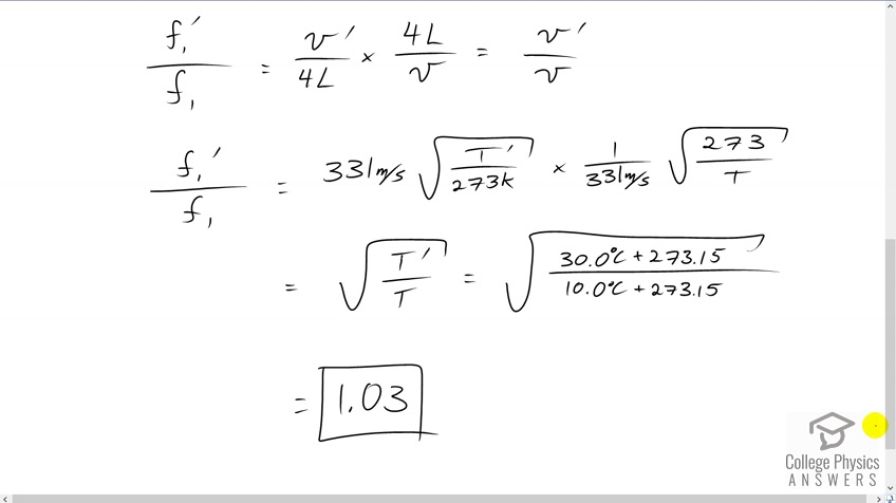
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to figure out the ratio of frequencies that a wind instrument will produce when the temperature inside the instrument changes from ten degrees Celsius to 30 degrees Celsius. So, lets suppose the wind instrument is can be modeled as a tube closed at one end, in that case the fundamental wavelength will have one quarter of it fitting within the length of the tube, which in this case the fundamental wavelength is four times L and knowing that the wave speed is frequency times wavelength, we can solve for frequency because we trying to find the ratio of two frequencies here so we need a formula for frequency in terms of wave speed and wavelength. So, the fundamental is going to be the wave speed divided by fundamental wavelength which is four L and then in the second case, when the temperature inside the instrument changes, so we call it f one prime, its going to be the new wave speed, we will call that v prime divided by the same length of the instrument, lets ignore the expansion of the metal as it gets warmer. We will assume that the wavelength is still four L. So, taking the ratio of these two frequencies is going to be the f prime which is v prime over four L divided by f one which is the fundamental at the original temperature and dividing by this fraction does the same as the multiplying by its reciprocal so you see the reciprocal of this written here. So, we are multiplying with four L over v and the four L cancel meaning we have v prime over v. So, substituting for wave speed and… and with this formula 331 meters per second times the square root of the temperature in kelvin divided by 273. So, this is the wave speed at 30 degrees Celsius and we will multiply it by reciprocal of wave speed at ten degrees Celsius and of course dividing by v is the same as multiplying by its reciprocal. So, that’s one over 331 times square root 273 over T and so this works out to… this works out for the square root of T prime over T, so that’s square root of 30 degrees Celsius converted into kelvin by adding 273.15 divided by ten degrees Celsius written in kelvin and all that works out to 1.03. So the ratio of frequencies is 1.03 and this is a three percent difference and so this is the minimum detectable frequency difference that we can perceive with the human ear and so it makes sense that wind instrument players tend to warm up their instruments before they really start to play it, because the frequency that the instrument produces will change as the air inside it gets warmer.
