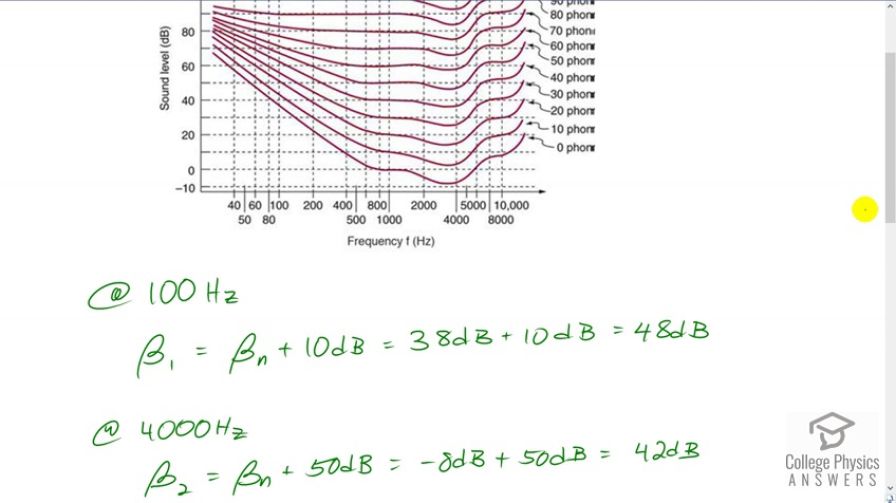
Question
A person has a hearing threshold 10 dB above normal at 100 Hz and 50 dB above normal at 4000 Hz. How much more intense must a 100-Hz tone be than a 4000-Hz tone if they are both barely audible to this person?
Final Answer
The 100 Hz tone must be 4 times as intense as the 4000 Hz tone.
Solution video
OpenStax College Physics, Chapter 17, Problem 69 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to figure out how many times or intense a barely audible sound at 100 hertz must be compared to a barely audible sound at 4000 hertz is for this person. The persons are a bit different because they have some hearing loss and at 100 hertz the hearing loss, is ten decibels hearing loss, we need to have ten decibels added to a normal sound level in order to have it barely audible and at 4000 hertz the bearing loss is such that they require an additional 50 decibels added to normal sound level to hear the same thing as normal hearing person would. So, since we are told that the sound is barely audible that means that the sound will be on this zero phons line and so we will figure out what is the sound level for a normal hearing person at 100 hertz and then we will add ten decibels there, to that, to find the sound level for this person with hearing loss. So, at 100 hertz we follow the graph straight up here along this we find, we find a 100 hertz on the x-axis and follow it up until we encounter the zero phons loudness line, the barely audible line and then figure out what sound level correspond to that frequency and that looks like it 38 decibels and then we have to add ten to that because of this person hearing loss and that means the sound level needs to be 48 decibels in order for this person to barely hear the 100 hertz sound. Now, 4000 hertz a person with normal hearing will require only about negative eight decibels sound level and now the hearing loss is, requires additional 50 decibels so we add 50 to negative eight and we got 42 decibels, must be the sound level for this person to barely hear a 4000 hertz sound. Okay. Now, we are going to find an expression for intensity in term of sound level and then we will divide the two intensities to find their ratio. So, sound level in general is ten times logarithm of intensity over some reference intensity and we can solve for I by first dividing both sides by ten and we get logarithm I over I naught equals beta over ten and then we will make both sides exponent of ten and on the left side, ten to the power of logarithm base ten of I over I naught, will be the argument, I over I naught and on the right hand side we have ten to the power of sound level over ten, then multiply both sides by I naught to get I, the intensity. Now, in this particular question we have, we want to find the ratio of I one over I two, the intensity at 100 hertz versus the intensity at 4000 hertz and so substituting for I using this formula here, we have I naught ten to power of beta one over ten nd I two is, I naught ten to power of beta two over ten and the I naught cancel and we are dividing powers of the same base and when you do that you can make a single exponent, which is the difference between the exponents and so we have ten to the power of beta one over ten minus beta two over ten and since they have a common denominator so we can write them both over ten, so its ten to the power of difference in sound level over ten and we found the sound level up here, 48 and 42 and so ten to the power of 48 minus 42 over ten is ten to the power three fifth and that is four. So, the intensity of the 100 hertz sound is about four times that of the intensity of the 4000 hertz sound.
