Question
(a) Echo times are measured by diagnostic ultrasound scanners to determine distances to reflecting surfaces in a patient. What is the difference in echo times for tissues that are 3.50 and 3.60 cm beneath the surface? (This difference is the minimum resolving time for the scanner to see details as small as 0.100 cm, or 1.00 mm. Discrimination of smaller time differences is needed to see smaller details.) (b) Discuss whether the period of this ultrasound must be smaller than the minimum time resolution. If so, what is the minimum frequency of the ultrasound and is that out of the normal range for diagnostic ultrasound?
Final Answer
Solution video
OpenStax College Physics, Chapter 17, Problem 79 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
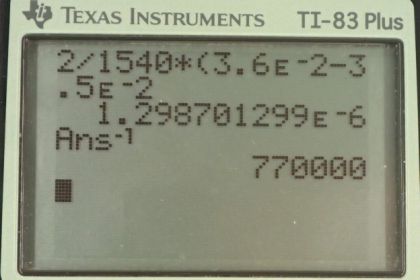
This is College Physics Answers with Shaun Dychko. Here is the surface of the skin, and some ultrasound is going down and it's going to bounce off this tissue here, this interface between two different types of tissue. This position is three and a half centimeters below the surface. So, we'll write that as D one equals three and a half times ten to the minus two meters. And then, the sum of the ultrasound will penetrate into the next layer of tissue, and then reflect off of this interface. And this position here is 3.6 times ten to the minus two meters. So, these two echoes will come back at slightly different times. So, the first echo will be here, and then the second echo comes from here. And, our question is to see what is the difference in time of measuring these two different echoes. So, the speed that ultrasound goes through the tissue which we know is 1540 meters per second is going to be two times the total distance that the ultrasound travels divided by the amount of time it takes. So, we know the distances because they're given to us. And, we'll solve this for T. Divide both sides by T over V, and you get this line here. And, it's the difference in times that we're interested in, so we want T two, which is the time for the echo to be received from this interface, and then minus T one, which is the time it takes for the echo to be measured from this interface. So, that's two D two over V minus two D one over V. They have a common factor two over V, which we'll factor out. So, two over V times D two minus D one is the time difference. And so, we plug in numbers. The time difference is two over the speed of ultrasound in tissue and then times by the difference in distances of the two tissue interfaces, and that gives 1.3 times ten to the minus six seconds. That's 1.3 milliseconds. Oh sorry, microseconds, I should say, which is a very short period of time. This is at the limit of what the electronics in the ultrasound detector can measure. Now, for part B, the wavelength of the ultrasound must be smaller than the detail that it's meant to observe, and so we'll figure out what the frequency then is by using this wave speed formula. So, the speed of sound is this minimum frequency times minimum wavelength. And, we can rewrite minimum frequency as one over minimum period. And then, we'll solve this for well, actually, we're just doing this. We're finding out what is the minimum frequency needed for this time difference. So we just take in the reciprocal of that time to get 0.7 megahertz. And, we're told that ultrasound of frequency between 0.8 megahertz and seven are used, and this rounds up to 0.8, so we'll see that yeah, that's within the typical frequency range.