Question
What intensity level does the sound in the preceding problem correspond to?
Final Answer
Solution video
OpenStax College Physics, Chapter 17, Problem 15 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
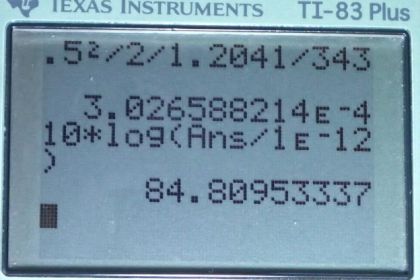
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We want to know the sound level of a sound that has a pressure amplitude of 0.5 Pascals traveling through air, and air has a density of 1.2041 kilograms per cubic meter. And the speed of sound and air is 343 meters per second when the air has a temperature of 20 degrees Celsius. So, we'll find the intensity first and then from that, we'll figure out the intensity level. Whenever you see the word level, intensity level, that level means find the decibels. So, we have a formula for intensity in terms of the sound pressure amplitude and that is the sound pressure amplitude squared divided by two times the density of the medium, which is air in this case, times the speed of sound in that medium. And so that is 0.5 Pascals and we square that divided by two times the density of air times the speed of sound of air. This gives 3.02659 watts per square meter. Now, the sound level is going to be ten times the logarithm of that intensity divided by the reference intensity, so that's ten times the logarithm of that answer divided by the reference intensity of ten to the negative 12 watts per square meter. And this gives 85 decibels.