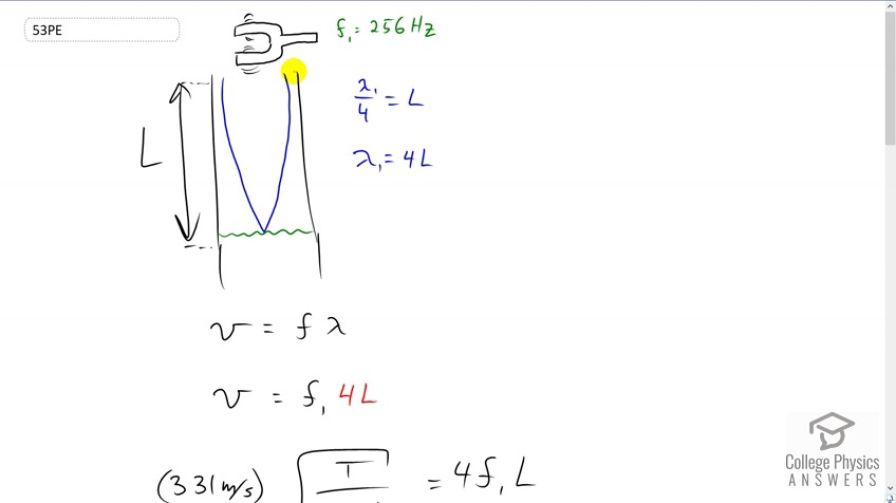
Question
(a) Students in a physics lab are asked to find the length of an air column in a tube closed at one end that has a fundamental frequency of 256 Hz. They hold the tube vertically and fill it with water to the top, then lower the water while a 256-Hz tuning fork is rung and listen for the first resonance. What is the air temperature if the resonance occurs for a length of 0.336 m? (b) At what length will they observe the second resonance (first overtone)?
Final Answer
- The next resonance occurs at . This is not an overtone, but rather a different resonant length for the same frequency. Overtones have higher frequencies.
Solution video
OpenStax College Physics, Chapter 17, Problem 53 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
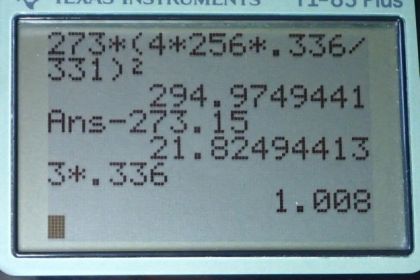
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a tuning fork with a fundamental frequency of 256 Hertz being put over top of the open end of this tube. And the tube has water in it and the water level is adjusted until there is a resonant frequency observed. And that will happen when this 256 Hertz sound becomes much louder than it normally is. And that is when this picture here when you have a coreture of the wavelength fitting within the tube. That is when you have the resonant length here. So, one quarter of the fundamental wavelength is going to be this length of this portion of the tube that has air in it. And we can solve this for lambda one by multiplying both sides by four. And we want that because we are going to come up with an expression that has temperature in it because we have to figure out what the air temperature is based on knowing this frequency and knowing what this length is. So, we can substitute for lambda one and write it as four L when we multiply it by f1 which is this given frequency of this tuning fork. And an expression for the speed of sound in terms of temperature is 331 meters per second times the square root of the temperature in Kelvin divided by 273. And that is going to equal to four f1 L because I just substitute it for v in this formula here. Normally I would have written it this in red but you got the idea. So divide both sides by 331 and you got the square root of T over 273 equals four f1 L over 331. And then square both sides and then multiply both sides by 273 and you get the temperature. So here is the temperature in terms of the length of the air column times by the frequency and so that is 273 Kelvin times four times fundamental frequency times length of the air column divided 331 squared. And 273 times four times 256 Hertz times 0.336 meters, this is the length that we are given and divide by 331 and square that and you get 294.97 Kelvin. from which we subtract 273.15 to turn into a more familiar 22 degrees Celsius. And question b says what is the next length at which resonance will be observed? And so the water can be removed from the tube until we have three quarters of a wavelength fitting in the tube. And you can see that this is going to be three times the length that we had for the fundamental wavelength. So there is a quarter of a wavelength, here is another quarter of a wavelength. And then here is another quarter of a wavelength, so that is three quarters. So that is going to be three times the fundamental which is 1.01 meters. Now the textbook calls this the first overtone, but that is not the correct term here because this frequency is the same as the frequency we had originally. This is just a different resonant length for the tube that will also resonate for the same frequency. Overtones are different frequencies.