Question
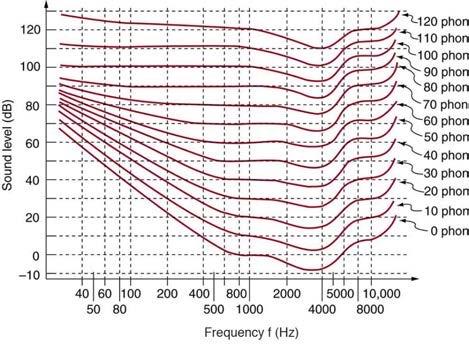
Based on the graph in Figure 17.35, what is the threshold of hearing in decibels for frequencies of 60, 400, 1000, 4000, and 15,000 Hz? Note that many AC electrical appliances produce 60 Hz, music is commonly 400 Hz, a reference frequency is 1000 Hz, your maximum sensitivity is near 4000 Hz, and many older TVs produce a 15,750 Hz whine.
Final Answer
60 Hz => 48 dB
400 Hz => 9 dB
1000 Hz => 0 dB
4000 => -8 dB
15000 => 17 dB
Solution video
OpenStax College Physics, Chapter 17, Problem 61 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. Each of the curve line here represents a single perceived loudness and so this zero phones line is the lowest loudness that is perceptible and so when you are looking at different frequencies, you can see that different number of decibels are needed to get a given loudness. So, if we had 60 hertz, we look here and we move up until we finally encounter the zero phones loudness line and read off what the decibel level is at that point, looks like it about 48, somewhere before just 50 and then at 400 hertz, we move up to the loudness, zero phones loudness line you can say and read across to the loudness level and its about… its about nine, well just under ten. So, this line, this tick mark here would be ten and yeah this is just before that dotted line leading to the tick mark, so its about nine and then at 1000 hertz, the threshold of hearing which is zero phones is at zero decibels and at 4000 hertz, you can have a… you can perceive a sound which has a sound level of negative eight decibels and so this is the frequency that is most easily perceived and then at 15000 hertz, which is somewhere over here, this is you know a non-linear scale by the way so we only this distance to go from ten to 15000 whereas over here, you know, that’s same kind of distance but that only adds a 100 hertz, here that is 5000 hertz. Its probably a logarithmic scale and we read up to the threshold of hearing and find the sound level and its about 17 decibels. There we go!