Question
Suppose a bat uses sound echoes to locate its insect prey, 3.00 m away. (See Figure 17.9.) (a) Calculate the echo times for temperatures of and . (b) What percent uncertainty does this cause for the bat in locating the insect? (c) Discuss the significance of this uncertainty and whether it could cause difficulties for the bat. (In practice, the bat continues to use sound as it closes in, eliminating most of any difficulties imposed by this and other effects, such as motion of the prey.)
Final Answer
- ,
- A uncertainty could be significant when catching small prey, or when it's important to bite a specific location such as the neck. Good thing the bat continually adjusts trajectory based on continuous use of echolocation while closing in.
Solution video
OpenStax College Physics, Chapter 17, Problem 11 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
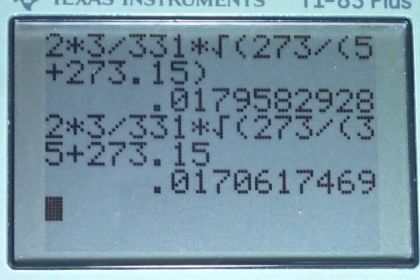
Calculator Screenshots
Video Transcript
This is College Physics Answers with Sean Dychko. This bat is using echolocation to locate this fly that it wants to eat. And suppose it separated from the prey by three meters. We're going to find what percent uncertainty exists if the air temperature is 35 degrees Celsius versus five degrees Celsius. So, let's find the times that it will take for the sound to return to the bat at those two different temperatures. So, the sound has to do a roundtrip to get to the bat. So, the bat emits a sound and then it bounces off the fly and returns to the bat. And so, the sound travels the separation distance between the bat and the insect two times. And so, this total distance is two times D, and that's going to equal the speed of sound multiplied by the time between emission and detection of the sound. Now the speed of sound as a function of air temperature is 331 meters per second times square root of temperature divided by 273 Kelvin. And this temperature has to be expressed in absolute temperature and Kelvin. And, we can substitute this in for V after we solve this for T by dividing both sides by V, and we get this line here. And then we'll substitute in for V so we're dividing by V, which is the same as multiplying by its reciprocal. So, the reciprocal of all this is one over 331, and that's why this is in the denominator. And then the reciprocal of this is the same thing but the fraction flipped over, so that's square root of 273 Kelvin over T. And so the temperature at five degrees Celsius is going to be two times three meters divided by 331 times the square root of 273 divided by five degrees Celsius converted into Kelvin by adding 273.15, and that makes a time of 0.0180 seconds. And then at 35 degrees Celsius, the speed of sound is slightly greater, and so we expect this time to be smaller, and so we have the same factor as before, multiplied by the square root 273 over 35 degrees Celsius plus 273, and that gives us a total time of 0.0171 seconds. So the percent uncertainty, you know, I don't know how precise the bat's thermometer is or its perception of air temperature and if it can account for these different times or different speeds of sound, but anyway. The percent uncertainty is going to be the difference between the two times divided by one of the times. So, it took the time at five seconds minus the time at 35 seconds, and the numbers are slightly different, because I'm doing a greater number, digits, in our calculations to avoid intermediate rounding error and dividing by the time five seconds and then multiplied by 100 percent to get a percent uncertainty of 5.01 percent. Now, 5 percent could be significant if you're catching something that's small, or when it's important to bite a specific location such as the creature's neck. But the bat is continually using echolocation as it closes in, and this percent uncertainty is going to be less and less the closer the bat is to the prey because you'll be dealing with smaller and smaller total times. And eventually, it will, it will find the place that it needs to find because of its continual use and adjustment.