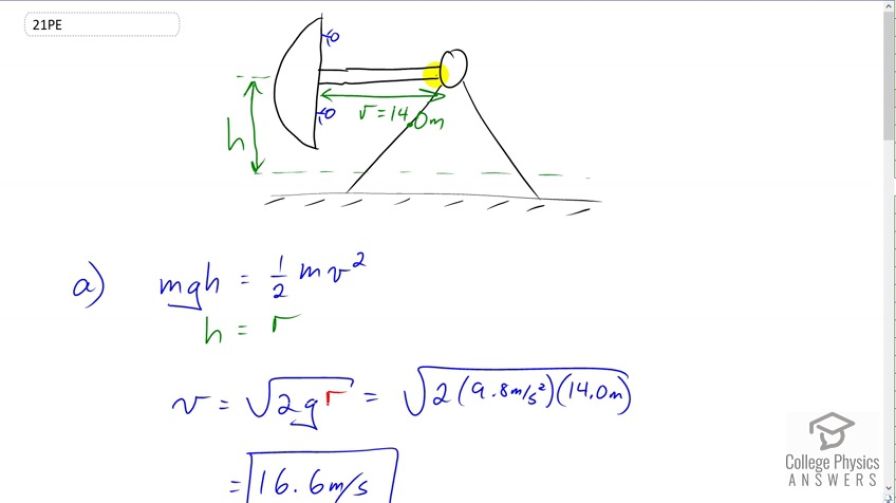
Riders in an amusement park ride shaped like a Viking ship hung from a large pivot are rotated back and forth like a rigid pendulum. Sometime near the middle of the ride, the ship is momentarily motionless at the top of its circular arc. The ship then swings down under the influence of gravity.
- Assuming negligible friction, find the speed of the riders at the bottom of its arc, given the system's center of mass travels in an arc having a radius of 14.0 m and the riders are near the center of mass.
- What is the centripetal acceleration at the bottom of the arc?
- Draw a free body diagram of the forces acting on a rider at the bottom of the arc.
- Find the force exerted by the ride on a 60.0 kg rider and compare it to her weight.
- Discuss whether the answer seems reasonable.
a)
b)
c) , is greater than by a factor of 3.
d) Yes, this is reasonable since it shoudl be greater than in order to accelerate the rider upwards, but not so much greater as to cause injury.
Solution video
OpenStax College Physics, Chapter 6, Problem 21 (Problems & Exercises)
Calculator Screenshots
Comments
This question is ridiculous. How is an introductory Physics student realistically going to be able to answer this correctly the first time? If this question involves concepts for chapter 7, it should be there instead.
This question is ridiculous. How is an introductory Physics student realistically going to be able to answer this correctly the first time? If this question involves concepts for chapter 7, it should be there instead.



