Question
The existence of the dwarf planet Pluto was proposed based on irregularities in Neptune's orbit. Pluto was subsequently discovered near its predicted position. But it now appears that the discovery was fortuitous, because Pluto is small and the irregularities in Neptune's orbit were not well known. To illustrate that Pluto has a minor effect on the orbit of Neptune compared with the closest planet to Neptune:
(a) Calculate the acceleration due to gravity at Neptune due to Pluto when they are apart, as they are at
present. The mass of Pluto is .
(b) Calculate the acceleration due to gravity at Neptune due to Uranus, presently about apart, and compare it with that due to Pluto. The mass of Uranus is .
Final Answer
Solution video
OpenStax College Physics, Chapter 6, Problem 40 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
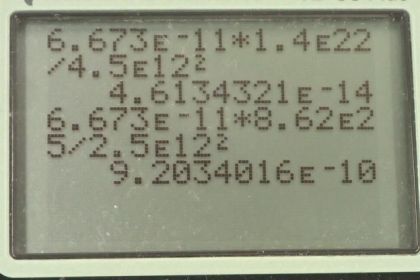
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The acceleration due to gravity on the surface of Neptune due to Pluto is going to be the gravitational constant multiplied by the mass of Pluto divided by the distance between Neptune and Pluto squared. So that's 6.673 times 10 to the minus 11 newton meters squared per kilogram squared times the mass of the Pluto divided by the Neptune-Pluto distance squared which is 4.6 times 10 to the minus 14 meters per second squared— that's a very small number. And the acceleration due to gravity on Neptune surface due to Uranus is this gravitational constant times the mass of Uranus divided by the Neptune-Uranus distance squared that gives 9.2 times 10 to the minus 10 meters per second squared. So we see that to put this acceleration due to gravity due to Pluto in context we can compare it with that due to Uranus and we see that the acceleration due to Uranus is 20,000 times greater than that due to Pluto.