OpenStax College Physics, Chapter 6, Problem 48 (Problems & Exercises)

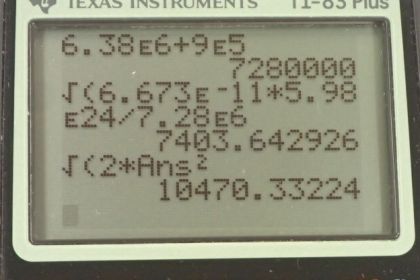
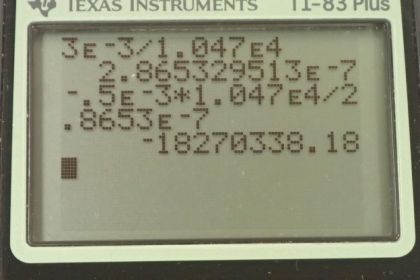
This is College Physics Answers with Shaun Dychko. A satellite is orbiting Earth and part A of this question asks, what is the speed of the satellite going to be? We know that the centripetal force is being provided by gravity. The centripetal force is the mass of the satellite times the speed squared divided by its radius. That's the radius from the center of its circle. That's going to equal gravity, which is the gravitational constant times the mass of the satellite times mass of the Earth divided by the distance from the center of the Earth squared. Now, the distance r here is going to be the radius of the Earth plus the distance above the surface that were given. We're told that the satellite orbits 900 kilometers above the surface of the Earth. I take this opportunity here when I'm writing down the information given to change units into MKS units, meters, kilograms, seconds. This 900 kilometers is now 9 times 10 to the 5 meters. The size of the rivet, that's going to come in the later part of this question, its diameter in other words, is 3 millimeters, which we'll call 3.00 times 10 to the minus 3 meters. The mass of the rivet is 0.5 grams, which we want to write in kilograms instead. That's 0.5 times 10 to the minus 3 kilograms. These are the kind of units that most of our formulas expect. Back to our question, part A here. We know that the Earth is here and the satellite is here. This distance from the surface has to be added to the radius of the Earth, and clearly this drawing is not to scale because the Earth would be much larger than this little distance above the surface. Any case, this total distance is r, it's the sum of the Earth's radius plus the distance above the surface, and it's 7.28 times in the 6 meters. We do some algebra on this equation here to solve for v, we'll multiply both sides by r. It cancels on the left and this is r to the power of 1 on the bottom there, and we'll divide both sides by mass of the satellite, and it cancels on both sides. We're left with v squared is Gm E over r. We take the square root of both sides and solve for v. The square root of Gm E over r. That's the square root of 6.673 times 10 to the minus 11 Newton meter squared per kilogram squared times 5.98 times 10 to the 24 kilograms, mass of the Earth, divided by 7.28 times 10 to the 6 meters from the center of the Earth to the satellite. That is 7.40 times 10 to the 3 meters per second, is the satellite's speed or the speed of anything else in orbit at that radius as well, including the rivet. Anything at this particular orbital radius is going to have the same speed because the speed depends on nothing else to do with a thing. It has nothing to do with the mass of the satellite or the rivet, it depends only on the distance from the center of the Earth and the mass of the Earth and the gravitational field constant obviously. There we go, part A done. Part B, there is a satellite orbit here, say, in green, and there is an orbit of this rivet, which is at 90 degrees. It says 90 degrees with respect to the Earth. But there are a lot of ways to intersect the satellite's path at 90 degrees with respect to the Earth. It could be intersecting this way or this way or this way. Anything that's in the plane of the drawing here would be at 90 degrees to the Earth. At 90 degrees to a line going into the center of the Earth it's parallel to the surface of the Earth at 90 degrees to a line going into the center of the Earth. At any case, we have to make an assumption about what that's supposed to mean. We're going to take this to be 90 degrees here. The rivet's velocity's gonna be at 90 degrees with respect to the satellite's velocity. We know the rivet is going to be moving parallel to the Earth's surface because it's in orbit just like the satellite is. It's not going to be cutting up to the orbit or down towards the Earth at all. Here we are, I've drawn each of these velocity vectors here. Here's velocity of the satellite with respect to the Earth. Here's the velocity of the rivet with respect to the Earth. They're going to have a collision. What we want to know in part B is what is the speed of the rivet compared to the satellite. What's the velocity of the rivet with respect to the satellite in other words. This is a relative velocity question. We're going to write out these other velocities with subscripts, two subscripts. The first denoting the thing is moving, and the second thing indicating what it's moving with respect to, or what this velocity is measured compared to. The velocity of the rivet with respect to the satellite is going to be the velocity of the rivet with respect to the Earth, which we know. Plus, we know it because everything has the same speed 7.40 times 10 to the 3 meters per second at this orbital radius. We're going to add to that the velocity of the Earth with respect to the satellite, which is the opposite to this velocity that we know here. We write it this way, because when the inner subscripts are the same, and when adding two different relative velocities, when the subscripts are the same, they cancel, and we're left with the other subjects. That's going to be the velocity of the rivet with respect to the satellite, which is what we want to find. The velocity of the Earth with respect to the satellite is just the opposite of the velocity of the satellite with respect to the Earth. I've drawn it to the left here for the velocity of the Earth with respect to the satellite, it's going to be the opposite direction. Now when we add these two vectors together, head to tail method, we have this resultant here, which is what we want to find. Now, the magnitude of these two components here are the same, because they're in the same orbital radius. They have to have the same speed. And they're at 90 degrees to each other. This resultant's going to be the Pythagorean sum of these two legs of this triangle. This is a way of saying that all these speeds are the same. The absolute value around a vector means speed. The speed of the rivet with respect to the satellite then is going to be the square root of the square of the velocity of the rivet with respect of the Earth, plus the velocity of the Earth with respect to the satellite. Then we replace each of these with the velocity of the satellite with respect to the Earth we found in part A, because everything orbiting at that radius has to have the same speed. It's square root of two times V se squared. It's square root of 2 times 7.4036 times 10 to the 3 meters per second squared, and that is 1.05 times 10 to the 4 meters per second. That's the speed of the rivet in the frame of reference of the satellite. Part C is asking for how long does it take for this rivet to impact the satellite. This impact occurs over what period of time. We have to make an assumption that the river does not pierce the satellite, which I think is a pretty not good assumption. I think it would probably blow a hole through the shell, the satellite. But anyway, we wouldn't be able to really answer the question if it did that. So we have to make this assumption in order to make the question answerable. We assume that this rivet is going to hit this side of the satellite and it's going to begin hitting when this edge of the rivet here touches the satellite and then it'll be finished hitting the satellite once this whole piece of metal squishes down to a flat pancake over this distance of 3 millimeters. The distance of this rivet traveling then, is its speed multiplied by time and we'll divide both sides by V rs. Then we solve for t. It's going to be rivet divided by its speed. Three times 10 to the minus 3 meters divided by the speed that we calculated in part B, that gives 2.87 times 10 to the minus 7 seconds. What speed is applied on the satellite due to the rivet? Sorry, what force I should say is applied on the satellite due to the rivet. The force on the rivet due to the satellite is the change of momentum of the rivet divided by time. That's the second law. It's a different way of expressing it. It was in fact, Newton's original way of expressing his second law was to say it's the rate of change of momentum is what force is, net force of course. This is going to be the expanding this change of momentum term. It's mass of the rivet times its final velocity which is zero, minus mass of the rivet times ITS initial velocity, all divided by time. This simplifies to negative m r V i over r since V f is zero. That's negative 0.5 times 10 to the minus 3 kilograms, the mass of the rivet, times its speed 1.0470 times 10 to the 4 minutes per second, divided by the-- By the way, it's a little mistake over here. Divided by the time that the rivet spins hitting the satellite, which we calculated in part C, 2.8653 times 10 to the minus 7 seconds. This works out to negative 1.83 times to the 7 newtons, and we take the positive of this to get the force on the satellite due to the rivet because that's going to be the Newton's third law counterpart to the force on the rivet due to the satellite. If you don't like this negative business and this Newton's third law business, you can safely ignore it. I mean, it's just being perhaps excessively rigorous and excessively technical. The force that the rivet experiences is the same magnitude force that the satellite experiences and that is 1.83 times 10 to the 7 newtons in the direction that the rivet was originally traveling. Part E, how much energy is generated by the collision? Well, there's no energy generated by it at all, but perhaps what it's asking is energy is changed from one form to the other. It has changed from kinetic into heat energy. I think the question is asking for how much heat energy is generated. The amount of thermal energy s going to be the opposite to the change in kinetic energy of the rivet. The change in kinetic energy of the rivet is one-half mV f squared minus one-half mass times the initial squared. That's one-half m times V f squared minus V i squared when you factor out the one-half m common factor. The final velocity is zero so it simplifies to negative one-half mV i squared. It's negative one-half times 0.5 times 10 to the minus 3 kilograms, times 1.047 times 10 to the 4 meters per second squared giving this many Joules. The thermal energy produced will be opposite of that change in kinetic energy. That is 2.74 times 10 to the 4 Joules.