Question
A fairground ride spins its occupants inside a flying saucer-shaped container. If the horizontal circular path the riders follow has an 8.00 m radius, at how many revolutions per minute will the riders be subjected to a centripetal acceleration whose magnitude is 1.50 times that due to gravity?
Question by OpenStax is licensed under CC BY 4.0
Final Answer

12.9 rpm12.9 \textrm{ rpm}

Solution video

OpenStax College Physics, Chapter 6, Problem 10 (Problems & Exercises)

OpenStax College Physics, Chapter 6, Problem 10 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

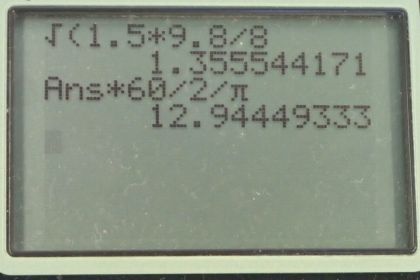
Calculator Screenshots

  • OpenStax College Physics, Chapter 6, Problem 10 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. This fair ground ride spins the occupants in a circle of radius 8.0 meters with an acceleration 1.50 times g. So we have to find the angular speed of this ride in rpm, or revolutions per minute. So centripetal acceleration is v squared over r but a better way to write it for this question is r times angular speed squared and then we can solve for this ω by dividing both sides by r... divide this by r and divide the acceleration by r and you are left with ω equals acceleration over r square rooted because we had to square root both sides to solve for ω. So it's gonna be the square root of 1.5 times 9.80 meters per second squared—that is the centripetal acceleration— divided by the radius of the path of the occupants which is 8.0 meters and square root that and you get 1.3555 and the units are radians per second. Then we convert that into revolutions per minute by multiplying by 60 seconds per minute. So that puts units of minutes in the denominator and then multiply by 1 revolution for every 2π radians and so we have 1.3555 times 60 divided by 2π gives us 12.9 revolutions per minute.

Comments

In the calculator picture - why did you divide by 2, and then divide by pi? this provides a different answer than if you divide by 2pi (which is what the formula uses)

Hi emilysims, thank you for the question, and good careful observation. It turns out there is no mistake. I could have put brackets around the denominator and multiplied 2 and pi together, which I think is that you're expecting. That would also give the correct answer and more visually resemble the formula. The calculator evaluates left-to-right, so it finds the result of the left part before going on to the next operation, assuming that each operation has the same precedence. For a concrete example, consider 62×3=1\dfrac{6}{2\times 3} = 1. That could be entered in the calculator as "6 / 2 / 3" and internally the calculator will evaluate "6 / 2" first, getting an intermediate result of "3", and then it will proceed to the next operation, which will be "3 / 3" (where "3" on the top is substituted for 6 / 2") and then get the answer "1". It's just a personal preference that I enter it as "6 / 2 / 3" instead of "6 / (2 * 3)" since the former involves less button pushing for the brackets.
All the best,
Shaun

Hi Shaun! Thanks for the thorough response! I finally realized that when I put "/2pi" in my calculator - I was actually dividing by 2 and then multiplying by pi. It's been a while, and I forgot about the impact of the order of operations in this moment. Thanks!

Hi shaun , how can you rewrite a=rw^2 from v^2/r on the very first step ? I don't quite understand

Hi hanjen, v=rωv = r \omega (equation 6.9). If we substitute for vv then we have ac=(rω)2r=rω2a_\textrm{c} = \dfrac{(r \omega)^2}{r} = r \omega^2 where one of the rr's canceled in the last step.
Hope that helps,
Shaun