Question
(a) Calculate Earth's mass given the acceleration due to gravity at the North Pole is and the radius of the Earth is 6371 km from center to pole.
(b) Compare this with the accepted value of .
Final Answer
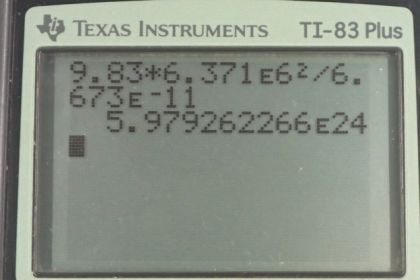
a)
b) This is the same as the accepted value to four significant figures.
Solution video
OpenStax College Physics, Chapter 6, Problem 33 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to calculate the mass of the earth given some data about the acceleration due to gravity at the North Pole which is 9.830 meters per second squared. The radius of the earth from Pole to Pole which is 6371 kilometers which we convert into meters to make 6.371 times ten to the six meters. This acceleration due to gravity is not quite the same as the usual version which we use which is 9.80. This is 9.83 and we'll see if using that number results in a different calculation for the mass of the earth. But we'll find in fact that given this radius also being different, these two differences compensate for each other to end up with the same mass of the earth that we would have calculated had we used data from the equator for example. So, the acceleration due to gravity at the pole equals the universal gravitational constant multiplied by the mass of the earth using data from the Pole, divided by the radius of the earth from Pole to Pole, squared. We'll solve this for m p by multiplying both sides by r p squared over g and then switch the sides around. We get mass of the earth is acceleration due to gravity at the Pole times the radius squared divided by g. So that's 9.830 meters per second squared, times 6.371 times ten to the six meters squared divided by 6.673 times ten to the minus eleven Newton meters squared per kilogram squared, giving us this value for the mass, 5.97926 times ten to the twenty-four kilograms and to four significant figures, this is the same as the accepted value for the mass of the earth.
Comments
can you remove the symbol for the little mass when not calculating satellites
Hi coleman, removing the little mass is OK whenever you're calculating the acceleration due to gravity for anything, whether or not it's a satellite. Acceleration due to gravity is , where is the mass of the planet causing the gravity and is the distance from the center of the planet to wherever the acceleration is occuring. As an exercise, try plugging in the mass of the Earth for and the radius of the Earth for and see what you get (it should be for the acceleration due to gravity on the Earth's surface).
All the best,
Shaun