Question
A geosynchronous Earth satellite is one that has an orbital period of precisely 1 day. Such orbits are useful for communication and weather observation because the satellite remains above the same point on Earth (provided it orbits in the equatorial plane in the same direction as Earth's rotation). Calculate the radius of such an orbit based on the data for the moon in Table 6.2.
Final Answer
Solution video
OpenStax College Physics, Chapter 6, Problem 43 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
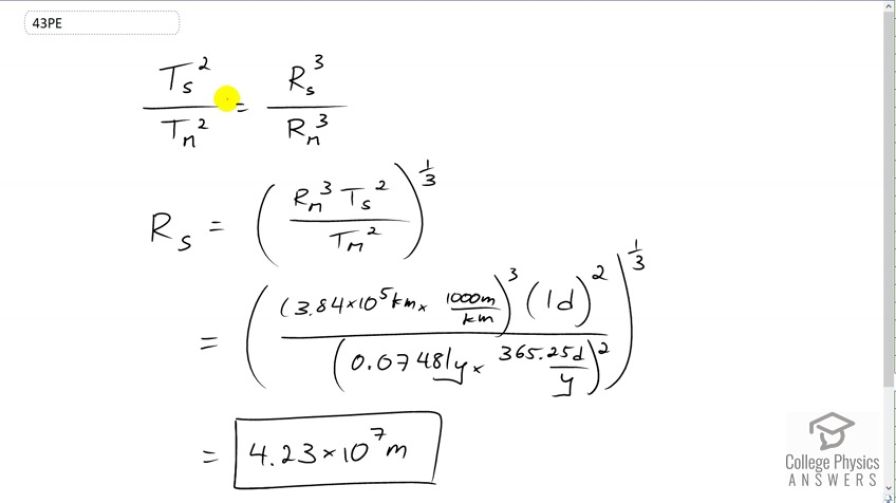
This is College Physics Answers with Shaun Dychko. We're going to find the radius of orbit for a satellite in a geosynchronous orbit. Since we're told to use Table 6.2 it means we are meant to use this Kepler's Law formula. So we're going to compare the period of the satellite to the period of the moon's orbit around the earth. We can do that because both the satellite and the moon, both orbit around the same thing, that being the earth. So this is why we chose data from the moon and didn't choose data for Jupiter around the sun for example because the sun would be the center of that, Jupiter's orbit, and that's not the same center as the satellite's orbit which is the earth. Okay. So, we have the period of the satellite's orbit squared divided by the period of the moon's orbit squared equals the radius of the satellite's orbit cubed, divided by the radius of the moon's orbit cubed. We can solve this for r s by multiplying both sides by radius of the moon's orbit cubed and then take the cube root of both sides or you could write that differently as raising both sides to the exponent one third, and then we plug in numbers. So we have 3.84 times ten to the five kilometers is the radius of the moon's orbit which we convert into meters and then cube that result, and then times by one day for the period of the satellite's orbit and which we don't have to convert into seconds. Often we have you know, meters, kilograms and seconds as units in our formulas but in this case we can leave it as days because then in the denominator if we also have that in days, the days squared at the top and days squared at the bottom will cancel. So we have 0.07481 years is the period of the orbit of the moon around the earth and we convert that into days by multiplying by 365 and a quarter days per year and this gives us 4.23 times ten to the seven meters must be the radius of the orbit of the satellite in geosynchronous orbit.
