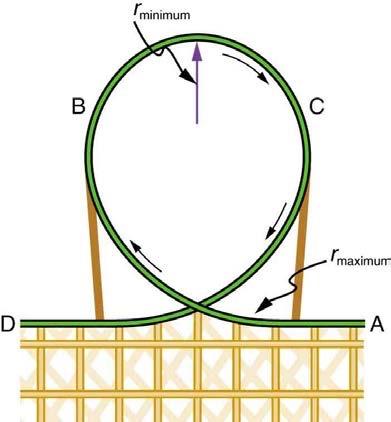
Modern roller coasters have vertical loops like the one shown in Figure 6.38. The radius of curvature is smaller at the top than on the sides so that the downward centripetal acceleration at the top will be greater than the acceleration due to gravity, keeping the passengers pressed firmly into their seats. What is the speed of the roller coaster at the top of the loop if the radius of curvature there is 15.0 m and the downward acceleration of the car is 1.50 g?

Video Transcript

This is College physics Answers with Shaun Dychko. We can rearrange the centripetal acceleration formula to solve for v. We multiply both sides by r and switch the sides around and also take the square root of both sides. So we have v equals the square root of the radius of curvature times the centripetal acceleration. So we're told that at the very top of the roller coaster loop, the radius of curvature is 15 meters and the acceleration is 1.5 times g and g is 9.8 meters per second squared. So we have 14.8 meters per second must be the speed at the top of the loop.