Question
Calculate the mass of the Sun based on data for Earth's orbit and compare the value obtained with the Sun's actual mass.
Final Answer
To three significant figures, the calculated value agrees with the accepted value for the mass of the sun.
Solution video
OpenStax College Physics, Chapter 6, Problem 44 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
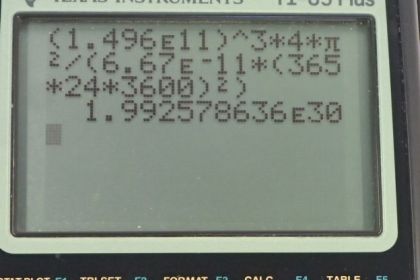
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to use data from the Earth's orbit around the Sun to calculate the mass of the Sun. So we know the gravitational force exerted by the Sun on the Earth is equal to the centripetal force and centripetal force is mass times r times the angular speed squared. So we can rearrange this to solve for m E and we are also going to substitute for this angular speed and replace it with 2π which is the number of radians in a full circle divided by the time it takes to do a full circle: the period of the Earth's orbit, in other words. So we have made that substitution here in red and I have canceled the mass of the Earth on both sides by dividing both sides by m E which is the same as multiplying by 1 over m E and we get this line here and then we'll solve for m S by multiplying both sides by r squared over the gravitational constant. And so we have r cubed—r squared times r makes r cubed here— and then this square here applies to everything inside the brackets so we have 4π squared and divided by T squared and also multiplied by G. So the mass of the Sun then is 1.496 times 10 to the 11 meters— that's the distance from the Earth to the Sun on average—cubed multiplied by 4π squared divided by the gravitational constant times the period expressed in seconds and we square that and we get 1.99 times 10 to the 30 kilograms and to three significant figures, this actually agrees very well with the accepted value.