Solution video
OpenStax College Physics, Chapter 6, Problem 25 (Problems & Exercises)
Calculator Screenshots
Comments
Are the answers in all problems shown with the correct number of significant figures??
Hi rileyhubsmith, thank you for the question. Yes, the final answers are rounded to the correct number of significant figures.
All the best,
Shaun
Why isn't friction taken into account? If there were no friction the car would slide off the road, correct?
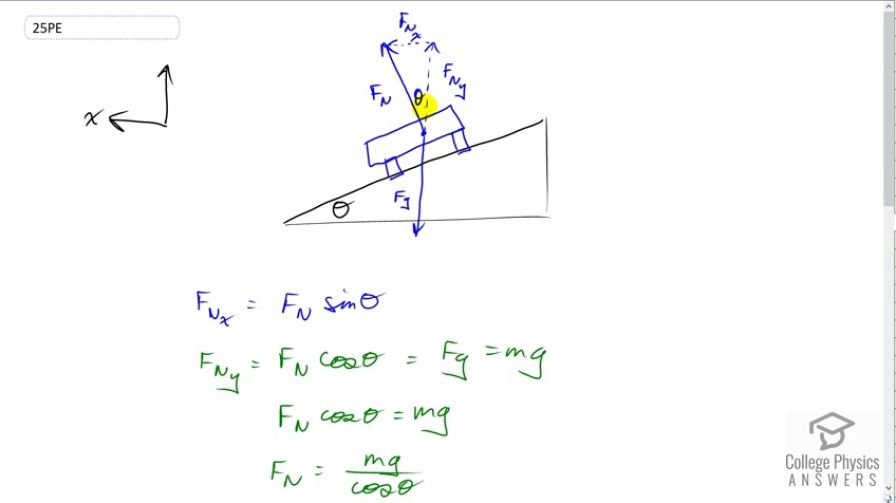
Hi e_than, thanks for the question. From here in the textbook: In an “ideally banked curve,” the angle ? is such that you can negotiate the curve at a certain speed without the aid of friction between the tires and the road.
I agree that it seems counter-intuitive that a car could negotiate a turn with zero friction. Consider what friction force would provide if it existed in this scenario? It would give a force perpendicular to the direction of motion that would change the direction of motion - make the car move along a curve. This curve is imagined to be part of a circle with the car velocity tangent to the circle and the force perpendicular to the velocity. The force, being perpendicular to velocity is directed toward the center of the circle (we know this because the tangent/radius angle is ninety degrees. The force is along the circle's radius in otherwords). Since the force is toward the center it is called centripetal.
The horizontal component of the normal force provided by the banked curve could be described the same way as a hypothetical friction force. The horizontal component of the normal force is directed perpendicular to the car's velocity, causing it to go along an arc of a circle (causing it to go around the turn, in other words). If the horizontal component of the normal force is large enough to provide make the car follow the turn, then friction isn't necessary. In the real world, friction is normally needed to supplement the horizontal component of the normal force.
Hope that wasn't too wordy and helps,
Shaun



