Change the chapter
Question
(a) Calculate the acceleration due to gravity on the surface of the Sun. (b) By what factor would your weight increase if you could stand on the Sun? (Never mind that you cannot.)
Question by OpenStax is licensed under CC BY 4.0.
Final Answer
  1. $274 \textrm{ m/s}^2$
  2. $28.0$
Solution Video

OpenStax College Physics Solution, Chapter 6, Problem 36 (Problems & Exercises) (2:08)

Sign up to view this solution video!

Start My Free Week
View sample solution

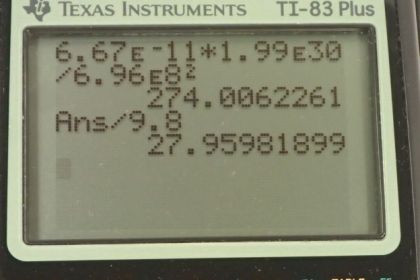
Calculator Screenshots

OpenStax College Physics, Chapter 6, Problem 36 (PE) calculator screenshot 1

Solutions for problems in chapter 6

1PE1AP2PE2AP3PE3AP4PE4AP5PE5AP6PE6AP7PE8PE10PE11PE12PE13PE14PE15PE16PE17PE18PE19PE20PE21PE22PE23PE24PE25PE26PE27PE28PE29PE30PE31PE32PE33PE34PE35PE36PE37PE38PE39PE40PE41PE42PE43PE44PE45PE46PE47PE48PE49PE