Question
At takeoff, a commercial jet has a 60.0 m/s speed. Its tires
have a diameter of 0.850 m.
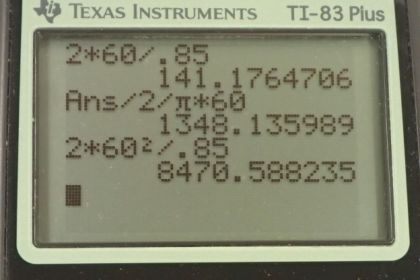
(a) At how many rev/min are the tires rotating?
(b) What is the centripetal acceleration at the edge of the tire?
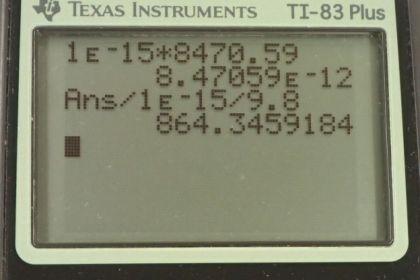
(c) With what force must a determined bacterium cling to the rim?
(d) Take the ratio of this force to the bacterium's weight.
Final Answer
Solution video
OpenStax College Physics, Chapter 6, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A jet is traveling at 60 meters per second on the runway and the diameter of one of their wheels is 0.85 meters, so that's the distance right across the wheel. The question is, what is the angular speed of the wheel? We take the linear speed of the point on the edge divided by the radius and that'll be the angular velocity. The radius is half the diameter. That's why we have d over 2 here substituted in place of r and multiply top and bottom by 2, and this 2 cancel with this one, and we're left with 2v over d. We have 2 times 60 meters per second divided by the diameter of 0.85 meters, and that gives 141.176 radians per second, but it asks us for an answer with units of revolutions per minute, rpm. We multiply this by 1 revolution for every 2 pi radians. Radiant units cancel. There are 2 pi radians in a revolution. Then we multiply by 60 seconds for every minute, nd we're left with revolutions per minute. The angular velocity of the wheel then is 1,350 rpm. In part B, we're going to figure out the centripetal acceleration of a point on the edge of the wheel. That is v squared over r, or v squared over half the diameter, or 2v squared over d, in other words. That's 2 times 60 meters per second squared, divided by 0.85 meters, which is 8.47 times 10 to the 3 meters per second squared. Then if some poor bacterium was on the edge of the wheel, on the treads, what centripetal force would be required to keep it stuck there? That is the mass of the bacterium 1 times 10 to the minus 15 kilograms, times this typical acceleration, and this works out to 8.47 10 to the minus 12 newtons. That may seem like a small number, but if we take this centripetal force as a ratio of its weight, we'll see that it's greater than its weight by a factor of 864. We take this centripetal force we calculated in part C and divide it by the mass of the bacterium times gravitational field strength, and we end up with 864.