Question
What is the ideal speed to take a 100 m radius curve banked at a angle?
Final Answer
Solution video
OpenStax College Physics, Chapter 6, Problem 26 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
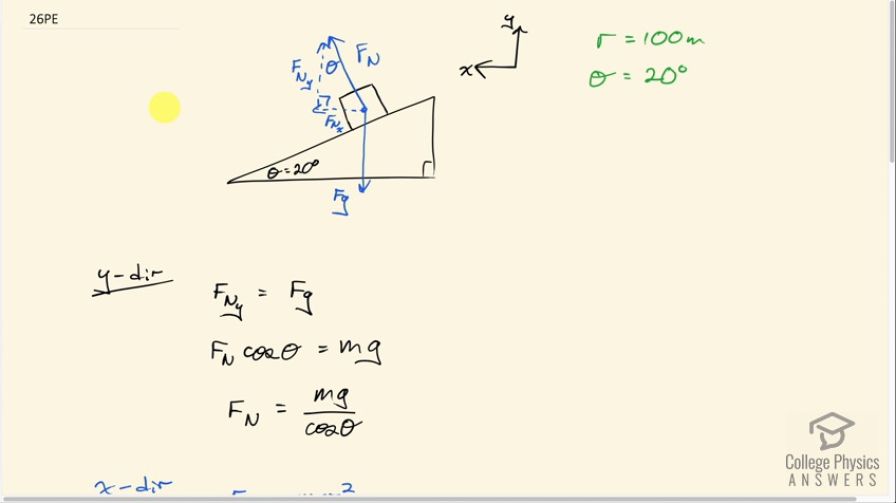
This is College Physics Answers with Shaun Dychko. This vehicle is taking this curve at the ideal speed and we have to figure out what that speed is given that the radius of curvature of their path is 100 meters and this is sort of a cross-section of the curve and the object is moving away from us let's suppose and this curve is banked at an angle of 20 degrees. So we are gonna have our x and y-axis straight up for y and straight to the left for the x-axis. Often in ramp or incline questions where we are dealing with friction, we would define our coordinate system to have x along the slope but that is not the case here because here we have some acceleration directly to the left as it goes in this curve. So the y-component of this normal force— the normal force being perpendicular to the surface here— its y-component has to equal gravity in order for their to be no vertical acceleration and its x-component is unbalanced because there is acceleration and that is centripetally towards the center of this curve that its traveling in and the x-component of the normal force then is what's providing that centripetal force. So let's begin with considering the y-direction to figure out what this normal force is. So the y-component of it is equal to gravity and that is to say that the normal force multiplied by cos Θ equals gravity which is mg and I'm using cos Θ because this y-component is the adjacent leg of this right triangle and we multiply cos of Θ then by the hypotenuse and then we solve for F N by dividing both sides by cos Θ so we have F N equals mg over cos Θ. I guess maybe it's a little bit tricky to know that this angle of incline here is the same as this angle up here. Let's suppose that you consider a line like this parallel to the incline in which case it's at 90 degrees to the normal force and you had a line going horizontally like this, this is going to be 20 degrees—I think that's pretty believable— I mean if you move this just down a little bit, you can see that it's mirroring this angle here. So that makes this full angle here the straight line angle of 180 degrees so that makes this portion in here, this wedge inside this triangle equal to 180 minus 90 minus Θ so that makes this 90 minus Θ, in other words, in here... that's 90 minus Θ. Well, these two have to add up to 90 so whatever this is— let's suppose we don't know what it is and we'll call it α— we know that α plus 90 minus Θ has to equal 90 because inside the triangle it has to be 180 degrees among all the angles 90 of which is taken up by this right angle here so leaving 90 leftover for these two angles. So we have α plus 90 minus Θ equals 90 and you can subtract 90 from both sides and we get 0 and then add Θ to both sides and you get α equal to Θ which is to say that this angle up here is Θ. Good... okay! So we have normal force is mg over cos Θ; we are gonna need to refer back to that in a minute... let's consider the x-direction. The centripetal force is the x-component of the normal force and another formula for it though is m times v squared over r and this v is what we are trying to find in the end. So here we equate the centripetal force with the x-component of the normal force and that is normal force times sin Θ because this is the opposite leg. And then we write this formula with the v on the left side so writing it as mv squared over r equals centripetal force but we wrote F Nsin Θ instead of F C. And then we solve for v squared by multiplying both sides by r over m and then we have v squared is rF Nsin Θ over m and then we finally go back to this result from the y-direction and substitute mg over cos Θ in place of the normal force. And this m cancels with this m and sin Θ divided by cos Θ is the same as tan Θ— and I suppose I could write that in red to show that it's a substitution— then take the square root of both sides and we have the speed then is square root of rgtan Θ. And this is called the ideal speed because this is speed that has no need for friction so there's no friction you can see in this free body diagram. Okay so the speed... the centripetal force is provided entirely by the x-component of the normal force, okay! So square root of 100 meters— radius of the curve— times 9.80 meters per second squared times tan 20 degrees and we get 18.9 meters per second.


