Question
What is the strength of the magnetic field created by the orbiting Moon, at the center of the orbit, in the system in the previous problem? (Treat the charge going around in orbit as a current loop.) How does this compare with the strength of the Earth's intrinsic magnetic field?
Final Answer
This is smaller than Earth's intrinsic magnetic field by a factor of .
Solution video
OpenStax College Physics for AP® Courses, Chapter 33, Problem 6 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
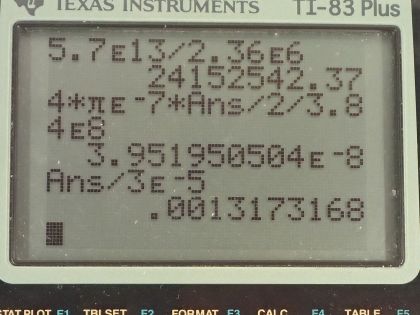
This is College Physics Answers with Shaun Dychko. In the previous problem, we figured out that the Moon should have a charge of 5.7 times 10 to the 13 coulombs on it. In this question, we are asked what would the magnetic field be at the center of the Moon's orbit and that is at the Earth given this charge on the Moon and given the speed that it's moving, so the speed that it's moving will affect the current that we'll imagine this Moon creating because this current is a current is moving charge and so this Moon is moving such that it completes one complete circle in a time of 2.36 times 10 to the 6 seconds— that's the period of the Moon's orbit and the current that it basically is is that amount of charge on the Moon divided by the time it takes to pass any particular point and so it takes 2.36 times 10 to the 6 seconds so we divide that into 5.7 times 10 to the 13 coulombs to get a current of 2.415 times 10 to the 7 amps. So that current is what we will substitute into this formula for the current at the center of a current carrying loop where we have the permeability of free space times the current divided by 2 times the radius of the loop and the radius would be the Earth-Moon distance. So the magnetic field then at the Earth due to the moving charge on the Moon is 4π times 10 to the minus 7 tesla meters per amp— that's permeability of free space— times the current divided by 2 times the Earth-Moon orbit which is 3.84 times 10 to the 8 meters and that's 4.0 times 10 to the minus 8 tesla. And then we compare that with the intrinsic magnetic field of the Earth and so we divide our answer by 3 times 10 to the minus 5 tesla and they got this number from the problem set in chapter 22 that tells us what to assume for the Earth magnetic field and the magnetic field that we have calculated is one one-thousandth of the Earth's magnetic field.