Question
How fast would two 7.0-kg bowling balls each have to be going in a collision to have enough spare energy to create a 0.10-kg tennis ball? (Ignore relativistic effects.) Can you explain why we don't see this in daily situations?
Final Answer
This isn't seen in everyday life since this speed is impractically high.
Solution video
OpenStax College Physics for AP® Courses, Chapter 33, Problem 10 (Test Prep for AP® Courses)
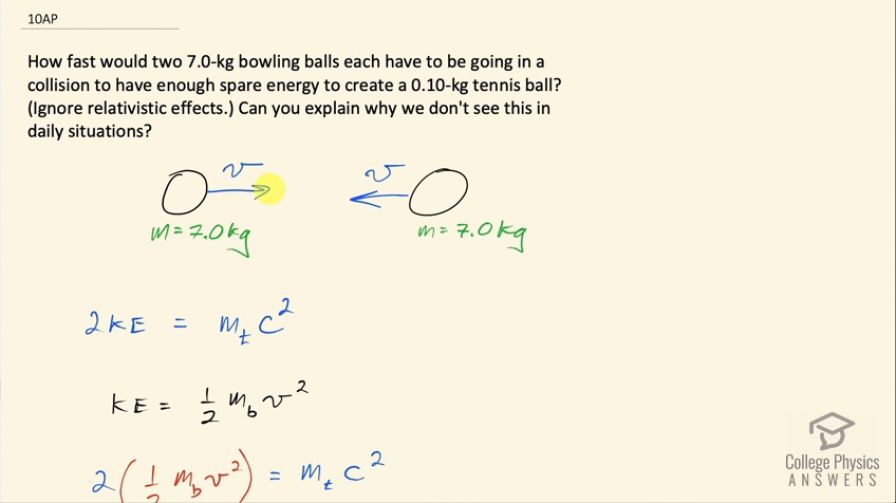
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Imagine two 7.0 kilogram bowling balls are approaching each other at some speed such that their collision can create a 0.10 kilogram tennis ball and the way this is possible is if their kinetic energy turns into the mass of this tennis ball and so each of these balls is going to have some kinetic energy and so 2 times the kinetic energy of one of them has to equal the mass of the tennis ball times c squared, this is the minimum kinetic energy needed to create the tennis ball. So the kinetic energy is going to be one-half times the mass of a bowling ball times its speed squared so we will substitute that in for KE and the 2 cancels with the one-half and we are left with mass of the bowl times the speed of the bowl squared equals mass of the tennis ball times speed of light squared. So we will divide both sides by the mass of the bowling ball and then take the square root of both sides and we get the speed of the bowling ball then has to be the square root of the mass of the tennis ball divided by mass of the bowling ball times C. So that's the square root of 0.10 kilograms divided by 7.0 kilograms and this works out to 0.12c and the reason we don't see this in everyday life is that it's unlikely for a bowling ball to achieve a speed like this.
