OpenStax College Physics for AP® Courses, Chapter 33, Problem 12 (Test Prep for AP® Courses)

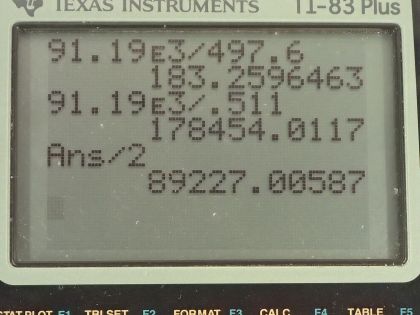
This is College Physics Answers with Shaun Dychko. We want to know how many K 0 particles can be created from a Z boson decay and also how many electrons and positrons could be produced this way? We need to look up the mass of the Z particle— it is 91.19 times 10 to the 3 megaelectron volts per c squared— and we should also do the same for the K 0 particle, which is 497.6 megaelectron volts per c squared. So we write those pieces of information down and the total energy of the Z particle has to equal some number that we want to calculate times the energy in each neutral kaon. So we substitute mass of the Z particle times c squared in place of the energy of the Z particle and that equals the number of neutral kaons times the mass of a kaon times c squared and we can divide both sides by c squared and also divide both sides by the mass of the neutral kaon and we get this expression here: the number will be the ratio of the masses. So 91.19 times 10 to the 3 megaelectron volts per c squared for the Z particle divided by 497.6 megaelectron volts per c squared that makes 183 of them. And then the question asks: how many electrons and positrons could you create? Well if you assume that the charge is going to be conserved then when we take the mass of Z boson and divide it by the mass of the electron or positron— they have the same mass— we get 1.78 times 10 to the 5 but that's the total number of particles total number of electrons and positrons. Now with charge being conserved, there will be in equal number of positrons and electrons in order to have a total net neutral charge that we started with with the Z boson and so we will divide this by 2 to get this number here: 89200 electrons and 89200 protons.