Question
Calculate the mass in of a virtual carrier particle that has a range limited to by the Heisenberg uncertainty principle. Such a particle might be involved in the unification of the strong and electroweak forces.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 33, Problem 2 (Problems & Exercises)
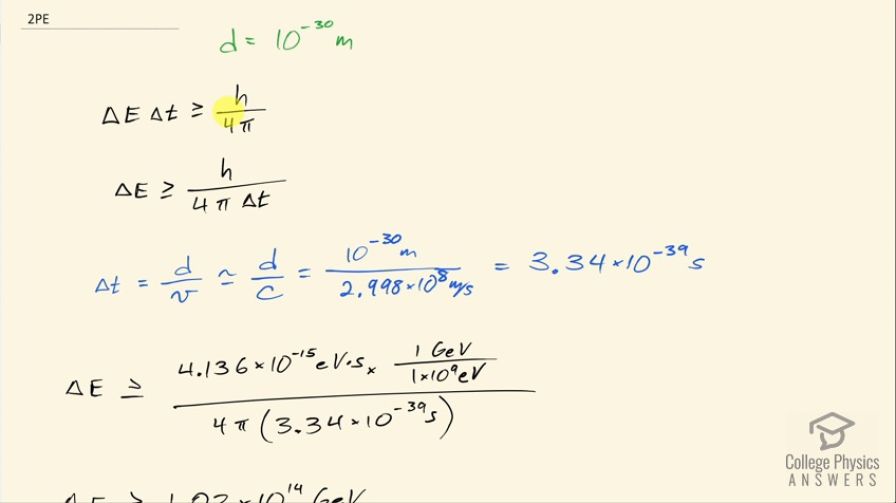
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to estimate the mass of a virtual carrier particle that has a range of about 10 to the minus 30 meters. We are going to use Heisenberg's uncertainty principle to figure this out. This says that the uncertainty in energy times the uncertainty in time is greater than or equal to Planck's constant divided by 4π. Now because this virtual carrier particle is virtual that means that it's violating conservation of energy and that's okay so long as its lifetime and its energy can sneak in... the product of those two things has to be less than Planck's constant over 4π. Now I say less than and I say that correctly... I know that there's a greater than or equal sign here this is talking about the real world that's measurable in that real world, the uncertainty in energy times the uncertainty in time has to be greater than or equal to Planck's constant over 4π and a sort of implication of this is that well anything's possible at a time and energy less than this fraction so in other words, conservation of energy can be violated so long as it sneaks in with a product of energy and time less than h over 4π. So we are going to turn this into an equal sign here this is going to be the maximum possible mass energy that the particle could have and it will be probably less than this Planck's constant over 4π times its lifetime, where I divided both sides here by Δt. Okay! So Δt is the time that this virtual particle spends traveling, it's going to go some distance d divided by its speed let's assume that its speed is approximately that of the speed of light so we are going to be minimizing this Δt and thereby maximizing our estimate for the mass-energy. So replacing v with c, we have 10 to the minus 30 meters divided by 2.998 times 10 to the 8 meters per second for an estimated lifetime of 3.34 times 10 to the minus 39 seconds. And so then this maximum possible energy that this particle could have is Planck's constant and I wrote this with units of electron volt seconds because we are asked to give an answer in gigaelectron volts per c squared. So we have 4.136 times 10 to the minus 15 electron volt seconds times 1 gigaelectron volt for every 10 to the 9 electron volts so now we have gigaelectron volt seconds in the numerator and we are dividing by 4π times the estimated lifetime of the particle in seconds, seconds cancel and we have 1.03 times 10 to the 14 gigaelectron volts. Again let's get rid of this greater than and we are calling this the maximum possible energy and E equals mc squared and so we can solve this for m by dividing both sides by c squared and so our estimated mass then is 1.0 times 10 to the 14 gigaelectron volts per c squared.
