Question
One decay mode for the eta-zero meson is .
(a) Find the energy released.
(b) What is the uncertainty in the energy due to the short
lifetime?
(c) Write the decay in terms of the constituent quarks.
(d) Verify that baryon number, lepton numbers, and charge are conserved.
Final Answer
- Please see the solution video
- Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 33, Problem 26 (Problems & Exercises)
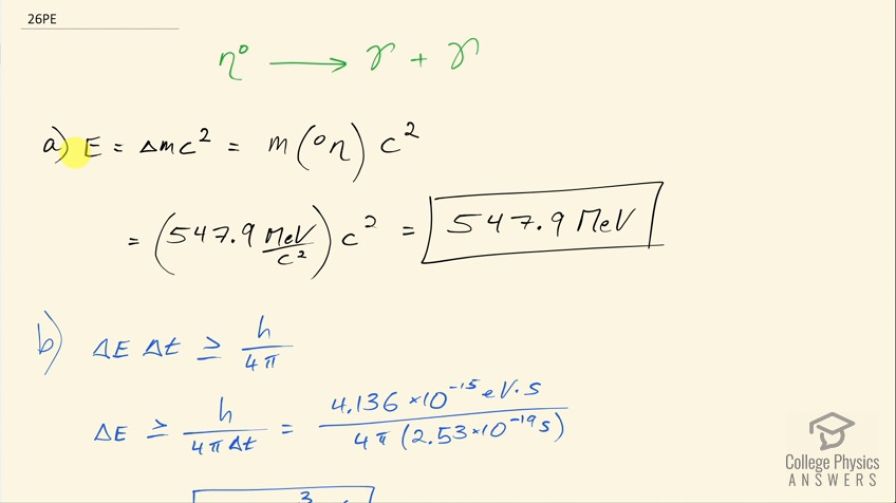
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The Eta zero particle can decay into two gamma particles and the question in part (a) is how much energy is released? So the energy released is the difference in mass between the reactants and products times c squared and the products have no mass, there's no rest mass in either of these gamma particles they are photons and so the change in mass is the mass that we start with in the Eta zero particle and so we look up that particle in table [33.2] and we can see that its mass is 547.9 megaelectron volts per c squared. So multiplying that by c squared means there are 547.9 megaelectron volts of energy released. Part (b) says what is the uncertainty in the energy released due to the short lifetime? So the product of uncertainty in energy and uncertainty in time is greater than or equal to Planck's constant over 4π— that's the Heisenberg uncertainty princple— and we will rearrange this to solve for the uncertainty in energy by dividing both sides by the uncertainty in time. And we will take the lifetime to be the uncertainty in time and that will give us a minimum uncertainty in energy when we take the maximum possible uncertainty in time being the lifetime. So we have the Planck's constant in units of electron volt seconds and we divide that by 4π times the lifetime, which we look up in this table as well 2.53 times 10 to the minus 19 seconds and then this is 1.3 times 10 to the 3 electron volts is the uncertainty in this energy released. In part (c) we are told to write the decay in terms of the constituent quarks. So the Eta zero particle is a rather strange one, it consists of a mixture of some of them being up and an up anti-quark and then other Eta zero particles might be a down quark mixed with a down anti-quark and in either case, it turns into photons. Part (d) says verify that baryon number, lepton numbers and charge are conserved. Well for each of these things, all the particles concerned have the number zero for all of them, there's no charge on any of these particles, there's no lepton number for any of them and there's no baryon number for any of them either so yes, it's conserved because it's zero all the time.
