Accelerators such as the Triangle Universities Meson Facility (TRIUMF) in British Columbia produce secondary beams of pions by having an intense primary proton beam strike a target. Such “meson factories” have been used for many years to study the interaction of pions with nuclei and, hence, the strong nuclear force. 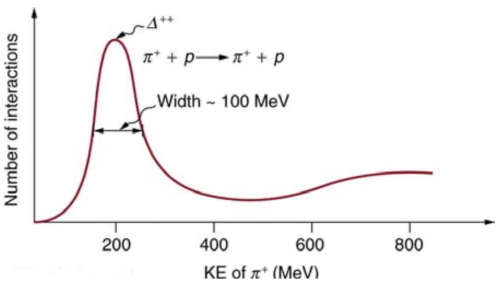One reaction that occurs is ${\pi }^{+}+p\to {\Delta }^{++}\to {\pi }^{+}+p$, where the ${\Delta }^{++}$ is a is a very short-lived particle. The graph in Figure 33.26 shows the probability of this reaction as a function of energy. The width of the bump is the uncertainty in energy due to the short lifetime of the ${\Delta }^{++}$. 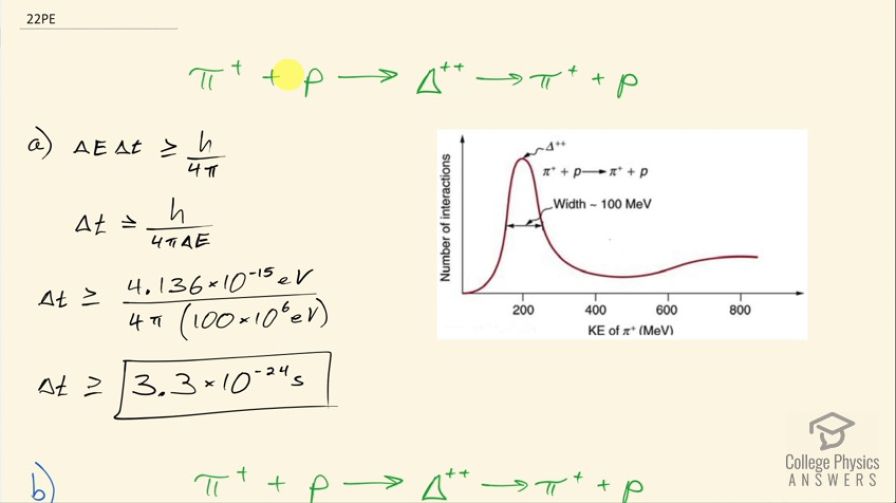(a) Find this lifetime. (b) Verify from the quark composition of the particles that this reaction annihilates and then re-creates a $d$ quark and a $\overline{d}$ antiquark by writing the reaction and decay in terms of quarks. (c) Draw a Feynman diagram of the production and decay of the ${\Delta }^{++}$ showing the individual quarks involved.

Video Transcript

This is College Physics Answers with Shaun Dychko. At the Triumph Facility at University of British Columbia, which is where I went to study Physics and education— great university— they have a facility that impacts protons into pions to produce a doubly charged Δ particle, which then quickly decays back into a pion and a proton. Part (a) of this question asks us to figure out what is the lifetime of this Δ particle? And it tells us what the approximate range of energies that this particle has and we will take this to be the ΔE in our Heisenberg uncertainty principle and we will use this to figure out what is the smallest possible lifetime that we could estimate for this particle. So we can rearrange to solve for Δt by dividing both sides by this uncertainty in energy and we get then that the lifetime of the particle is greater than or equal to Planck's constant divided by 4π times the uncertainty in the energy. So that's 4.136 times 10 to the minus 15 electron volt seconds divided by 4π times 100 megaelectron volts, which is what we are told the width is and that's 100 times 10 to the 6 electron volts and the electron volts cancel leaving us with a lifetime in seconds. So it's going to be at least 3.3 times 10 to the minus 24 seconds. Part (b) asks us to verify that a down quark and an anti-down quark or a down anti-quark, you might say annihilate to form, well, nothing and then we are left with this particle that has three up quarks and then what ensues after that is a reversal of that annihilation whereby a down anti-quark and a down quark are produced and create these down, up, up particle, which is a proton and then a down anti-quark up quark, which is the positive pion so there we go that's that picture. And part (c) asks us to show a Feynman diagram depicting the production and decay of this Δ ++ particle. So we start off with a proton that has an up, up, down quark and then a positive pion within down anti-quark and an up quark and this horizontal access is positioned so these two particles are in different positions here because they are horizontally separated and then as time progresses, they will interact such that the down and the down anti-quark meet here and annihilate leaving us only with these three up quarks left over which comprise this Δ ++ particle. And then some time further still as we go up, we have some interaction happening— that's what the squiggle represents— which causes somehow this down anti-quark and this down quark to appear and then we have a positive pion and a proton again.