Question
The decay mode of the negative muon is
.
(a) Find the energy released in MeV.
(b) Verify that charge and lepton family numbers are conserved.
Final Answer
- Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 33, Problem 16 (Problems & Exercises)
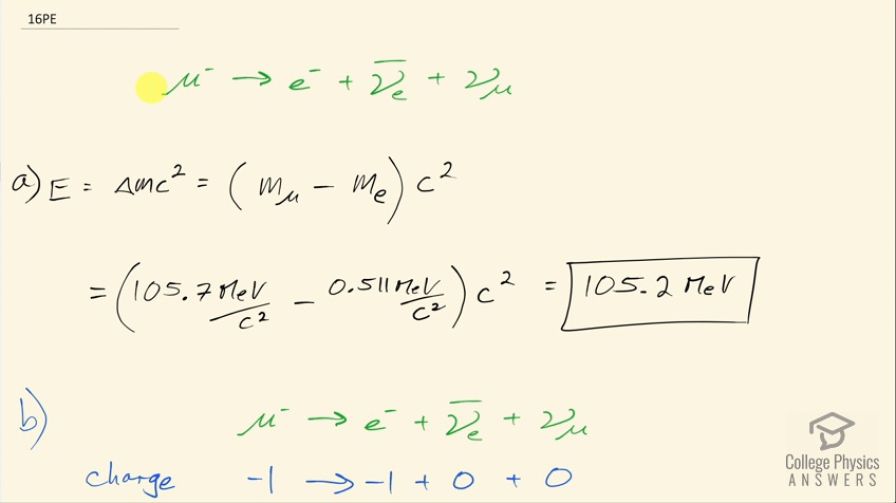
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A muon can decay into an electron, an electron anti-neutrino and a muon neutrino and the question is how much energy is released in this decay? So the energy released then is going to be the difference in mass between the reactant and the products times c squared. So that will be the mass of the muon minus the mass of the electron times c squared and the electron anti-neutrino and the muon neutrino are both massless. So we look up in table [33.2] for the masses here, muon has a mass of 105.7 megaelectron volts per c squared and the electron has a mass of 0.511 so we put these numbers in here and we end up with 105.2 megaelectron volts of energy released. Part (b) asks us to verify that the charge and lepton family numbers are conserved. So let's look at charge first: on left side, we have negative 1 and on the right hand side, we have negative 1 for the electron and 0 for each of the neutrino and anti-neutrinos so that checks out, it's negative 1 on both sides so that means it's conserved— it's the same on both sides— and there are two different types of leptons so the first type is the muon so the muon family number is 1 on the left because this is a matter muon and over here, we have a regular matter muon neutrino, which also has a positive 1 muon family number and so it's 1 on both sides so that checks out. And then for the electron family number, we have 0 on the left side because there are no electrons on the left side or electron neutrinos and on the right hand side, we have an electron which is regular matter so it has an electron family number of positive 1 and then we have an electron anti-neutrino and being anti-matter, it has an electron family of negative 1 so 1 and negative 1 makes 0 on the right, which is the same as the total 0 we had on the left and that also checks out.
