Question
The primary decay mode for the negative pion is . (a) What is the energy release in MeV in this decay?
(b) Using conservation of momentum, how much energy does each of the decay products receive, given the is at rest when it decays? You may assume the muon
antineutrino is massless and has momentum , just like a photon.
Final Answer
- ,
Solution video
OpenStax College Physics for AP® Courses, Chapter 33, Problem 47 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
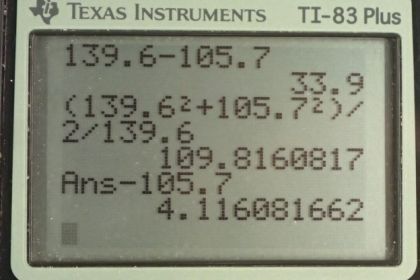
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The negative pion decays into a muon and a muon anti-neutrino so the question in part (a) is how much energy is released in this decay? So we find the difference in mass of the products and the reactant. So what is the difference between the negative pion to begin with and the mass of the muon on the product side; this neutrino is essentially massless. So we have 139.6 megaelectron volts per c squared for the negative pion minus 105.7 megaelectron volts per c squared for the muon and take that difference, multiply it by c squared and you end up with 33.9 megaelectron volts of energy released. Now question (b) says how much of that energy gets turned into kinetic energy of the muon and kinetic energy of the anti-neutrino? So we use conservation of momentum in order to figure out how the energy will be divided between these two particles. Well so first of all we noticed that the total momentum to begin with is zero because we are told that this negative pion is at rest so there's no momentum initially. So that must mean that total momentum after decay has to also be zero and in which case, the momenta has to be of equal magnitude and opposite directions in order for their total to be zero. So that means the magnitude— that's what the vertical absolute value signs are meant to indicate— the magnitude of the muon momentum is the same as the magnitude of the anti-neutrino momentum and we'll just call it p; there's no need to distinguish between that of the muon and the neutrino because they are the same, just in opposite directions. So we are told that the neutrino momentum will be treated as a photon momentum because it's essentially massless and so it will be its energy divided by c and I had a subscript here but I am showing that that's not needed since it has the same momentum as the muon. Now for the muon, it's energy squared is gonna be its momentum squared times c squared plus its rest mass squared and well rest mass energy after you multiply by c squared. And there's no need to have this subscript here so I rewrote it without that subscript. And then I also rewrote this equation in this form in order to see that after you multiply both sides by c here and then square both sides, we end up with this form here where the energy of the neutrino squared is momentum squared times c squared and this becomes something we can substitute in up here. But before we get to that, let's also notice that the energy of the muon plus the energy of the neutrino has to total the energy of the pion that we started with and keep in mind that this energy is the total energy the kinetic energy plus its mass energy. So the total energy of the muon plus the total energy of the neutrino equals the energy of the pion that we started with and this energy of the pion since it's at rest and it has no momentum is just its rest mass energy so that's mass of the pion times c squared. So let's do some substitutions now that we have collected these facts here. We have the energy of the muon squared then we can replace p squared c squared with energy of the neutrino squared plus this copied down, rest mass energy of the muon squared and then this in turn can be substituted from here we can say that the energy of the neutrino is the mass energy of the pion minus the energy of the muon. So we make that substitution here and that's squared and then we carry out this square of this binomial and we end up with m πc squared squared minus 2 times energy of the muon times m πc squared plus energy of the muon squared plus this term copied. And we see that there's an energy of the muon squared term on both sides which is fortunate for our algebra work because then this term disappears from both sides. And then we isolate this term because it contains the thing we want to know which is the total energy of the muon we bring that to the left side and it becomes positive 2 E μm πc squared equals all this stuff here just copied and then we divide both sides by these factors that are being multiplied by the energy of the muon. So the total energy of the muon then is the mass energy of the pion squared plus the mass energy of the muon squared divided by 2 times the mass energy of the pion and so we look up these masses in our data table and we have 139.6 megaelectron volts per c squared times c squared for the negative pion and we square that result plus the mass energy of the muon squared divided by 2 times the mass energy of the pion and this gives 109.8161 megaelectron volts. Now that is the total energy of the muon. Now its kinetic energy is going to be this total energy that we found minus its rest mass energy. So that's a 109.8161 that we found here minus the 105.7 that we can look up in the data table and we end up with 4.1 megaelectron volts is the kinetic energy of the muon. So that means everything else has to be all the rest of the energy that we started with and we started with this much energy in the pion to begin with all the rest of the energy has to go to the anti-neutrino. So we have 139.6 megaelectron volts per c squared times c squared— that's the energy of the pion— minus the total energy given to the muon that is its kinetic energy plus its rest mass energy and we take this difference and we end up with 29.8 megaelectron volts must be the energy of the muon anti-neutrino and this energy will be its well kinetic energy you could say I suppose althought it's a bit hard to distinguish between kinetic energy and rest mass energy because it has no rest mass. So anyhow it is the energies of these two particles; 4.1 megaelectron volts kinetic energy for the muon and 29.8 megaelectron volts energy for the muon anti-neutrino.