Question
What is the ideal banking angle for a gentle turn of 1.20 km radius on a highway with a 105 km/h speed limit (about 65 mi/h), assuming everyone travels at the limit?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 6, Problem 25 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
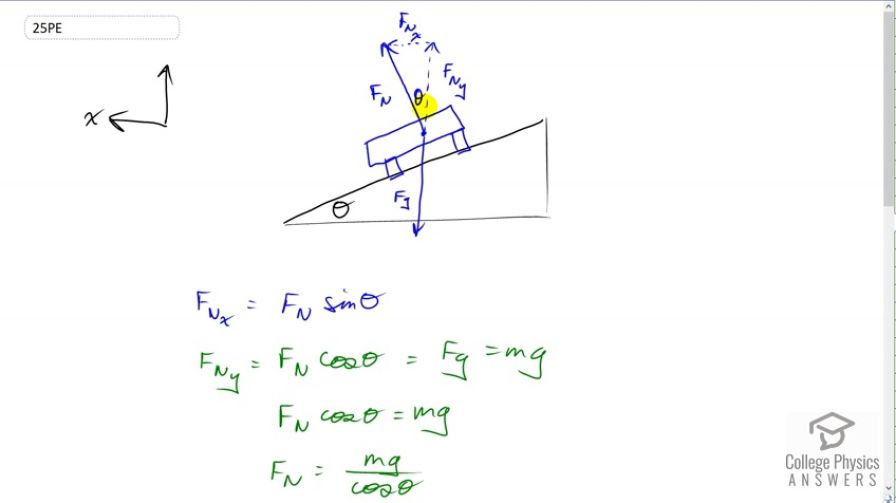
This is College Physics Answers with Shaun Dychko. This car is accelerating around this curve. It's going at constant speed, but it is never the less accelerating since its velocity is changing direction. So we have centripetal acceleration in other words and that's caused by this component of the normal force which is directed towards the center of the curved path. So this angle here is theta and we can use normal force multiplied by sine of theta to find this component in the x direction or radial component. We know this is theta because you can imagine this line here parallel to the ramp and then you can imagine another line here which is horizontal and this would be theta because these would be interior opposite angles. With that being theta and this being 90 because this is a normal force which is perpendicular to the surface of the ramp, this dot here plus theta has to add up to 90. But this dot here plus whatever this angle is here, let's assume we don't know it's theta yet, also has to make 90 since this F n y is pointing straight up and that makes a 90 degree angle there. So if this dot plus theta makes 90 and this dot plus the angle in here also makes 90, that means this must equal that and so it is theta in there. All right. So the y component of the normal force is the normal force multiplied by cosine theta because the y component is the adjacent leg of this triangle. We know that that has to balance gravity. So that's vertical, this F n y is vertically upwards and so it has to balance the m g force of gravity downwards. That means F n cos theta is m g. We can solve for F n by dividing both sides by cos theta . That gives F n is m g over cos theta and the reason that's useful is we can substitute that back into this formula replacing F n in the F n x formula in order to well, eventually solve for theta. But let's take it one step at a time. So re-writing F n x and noticing that it is the centripetal force, in which case it must be m v squared over r because that's the formula for centripetal force. Now we can say that m v squared over r is this expression we had before for F n x which is F n sine theta. But now we'll replace F n with what we figured out in this part here in green, m g over cos theta times sine theta. Now sine theta over cos theta can be written as tan theta and we'll divide both sides by m as well. We have v squared over r equals g tan theta. Then divide both sides by g and you get tan theta is v squared over r g. That means theta is the inverse tangent of v squared over r g. So that's the inverse tangent of 105 kilometers per hour converted into meters per second and then square that, and divide by 1.2 kilometers converted into meters, times 9.8 meters per second squared. This all gives 4.14 degrees is the ideal banking angle for this particular speed and this radius of curvature. This assumes there is no friction by the way.
