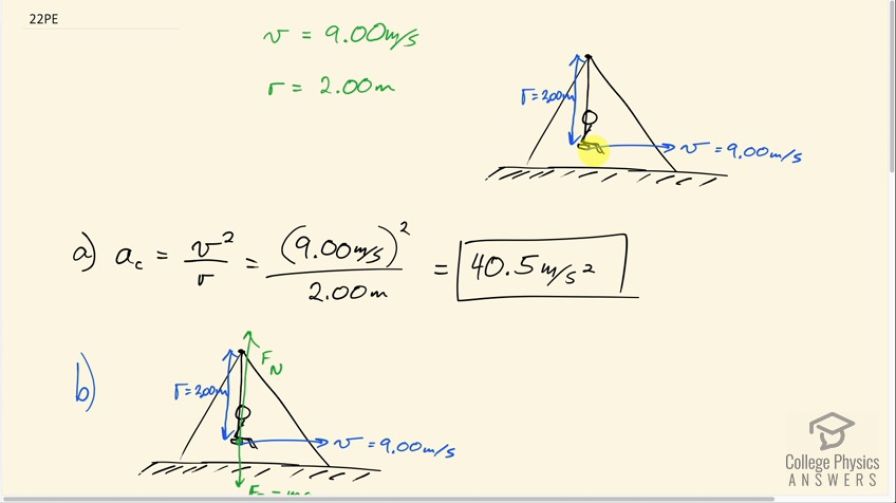
A mother pushes her child on a swing so that his speed is 9.00 m/s at the lowest point of his path. The swing is suspended 2.00 m above the child's center of mass. (a) What is the magnitude of the centripetal acceleration of the child at the low point? (b) What is the magnitude of the force the child exerts on the seat if his mass is 18.0 kg? (c) What is unreasonable about these results? (d) Which premises are unreasonable or inconsistent?

Video Transcript

This is College Physics Answers with Shaun Dychko. This child on a swing is traveling with a tangential velocity of 9.00 meters per second at the bottom of the swing, allegedly, and their center of mass is 2.00 meters from the pivot here at the top of the swing. So finding their centripetal acceleration, the formula is the linear speed squared divided by the radius. So that's 9.00 meters per second squared divided by 2.00 meters which is 40.5 meters per second squared. In part (b), we are asked what is the force the child applies on the swing and the magnitude of that force is gonna be the same as the normal force because these are Newton's third law pairs so the normal force upwards on the child is of equal magnitude to the force downwards on the swing which I haven't drawn here but a dot sort of on the swing itself going down this would be the force on the seat of the swing. Okay! So Newton's second law says that the force upwards which is the normal force minus the force downwards which is gravity equals mass times acceleration. In this case, we put a subscript c on the acceleration just because it's a circular motion scenario but it is Newton's second law just the same, you don't have to write the c. Okay but let's put it back! So in order to answer our question, we find the normal force and that would be the force exerted on the seat. So normal force is mass times acceleration plus force of gravity moving this term to the right hand side by adding it to both sides and the force of gravity is mass times acceleration due to gravity. So we can factor out this common factor m and then plug in numbers. So the normal force is 18.0 kilograms times 40.5 meters per second squared that we found in part (a) plus 9.8 meters per second squared which is a force of 905 newtons. Now in order to decide whether that's a reasonable number or not, we have to compare it to something relevant: let's compare it to the child's weight. So we'll take that normal force—905 newtons— divide it by the child's weight which is 18.0 kilograms times 9.80 newtons per kilogram which is 5.1 and it seems to me that 5.1 is excessive. So the force exerted by the swing is 5.1 times the child's weight—that's too much. Then the swing speed is overstated; it's not reasonable to presume that they are going 9.00 meters per second.