OpenStax College Physics for AP® Courses, Chapter 6, Problem 30 (Problems & Exercises)

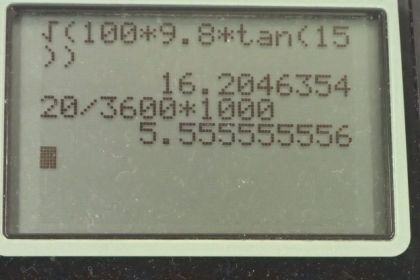
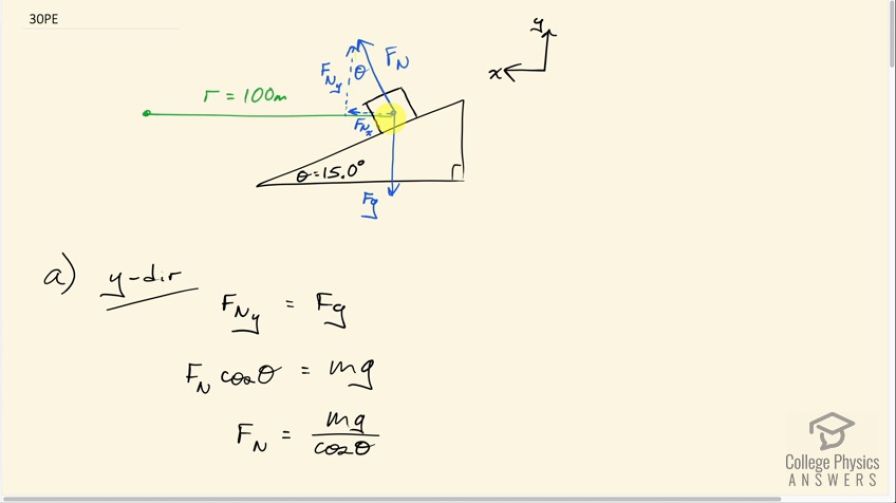
This is College Physics Answers with Shaun Dychko. Welcome to Question 30! You should be congratulating yourself for clicking "Play" on this video because it's a long one and it's very interesting especially when we get to part (b) when we have friction so fasten your seat belt, here we go! In part (a), we are told that there's no friction and we are asked to find what the ideal speed for this car to go around this curve— it's a banked curve— and the ideal speed being the speed at which there's no sliding up or down the ramp and there being no friction. So we have our coordinate system oriented such that the y-axis is straight up and the x-axis is straight to the side... that's a little bit different than other incline questions we have done where we have tilted the x and y axis to be along the ramp and perpendicular to the ramp respectively but we are not doing that here; instead we have straight up and straight to the side. So that means this normal force now has a y-component straight upwards and a x-component straight to the side and there are no other forces acting on this car. This car—I mean I drew it as a box but you can imagine that it's a car— and it's going away from us in this picture or towards us, hard to tell. Okay! So we know that the x-component of this normal force is gonna be providing the centripetal force— it is the centripetal force, in other words— and the y-component of this normal force has to exactly balance gravity which is straight down and so that's what we said here so the y-component of the normal force equals gravity. So that is the normal force, F N, multiplied by cosine of Θ because this is the adjacent leg of this right triangle and we use cos Θ multiplied by the hypotenuse to get this adjacent leg. And then gravity is mg and we can solve for the normal force and say that it's mg over cos Θ and I did that just because it's probably useful for the next part in the x-direction because it's gonna be another equation involving the normal force and if we have two equation's and two things that we don't know then we'll be able to combine the two equation's and solve for our answer. Okay! So the x-component of the normal force is mass times acceleration—this is Newton's second law. You could put a little subscript c here to say it's centripetal acceleration but it is acceleration just the same and we have a formula for it though in the centripetal case which is the speed squared divided by the radius of curvature. So we also have a substitution for the x-component of the normal force which is to say that it's F N times sin Θ because it's the opposite leg of this triangle. So we substitute both of these parts in black and we do that in red in this blue equation. So acceleration has been replaced with v squared over r and the x-component of the normal force has been replaced with F Nsin Θ. And then we solve for v squared by multiplying both sides by r over m and we get the v squared is rF Nsin Θ divided by m. And so here's an equation with two unknowns: we don't know v and we don't know F N and so we need to return to the work we did here and make a substitution for F N and it's mg over cos Θ. So we have rmg over cos Θ times sin Θ over m and these m's cancel and sin Θ divided by cos Θ is the same as tangent Θ and so we have v squared is rgtan Θ and so we can take the square root of both sides to solve for v. So v is square root rgtan Θ which is a square root of 100 meters times 9.80 meters per second squared times tan of 15 degrees which is 16.2 meters per second. Now in part (b), we say suppose a driver who is scared of the curve takes it at a speed less than 16.2 meters per second; they take it at 20 kilometers per hour which after converting into meters per second by multiplying by 1 hour for every 3600 seconds and by 1000 meters for every kilometer, it is 5.5555 meters per second which is significantly less than this. And what that will mean is that, you know, if there was no friction then this centripetal force, which you know is going to be the same regardless of the speed of the car, it's gonna be enough to actually move it too much towards the center of the circle and it will accelerate it more than necessary to go in in its curve and so it will slide down the ramp as a result. So to compensate for that, we need a friction force which is always parallel to the interface between the two surfaces and so it's going to be up and parallel to the ramp, or the banked curve I should say, and this friction force has a x-component and a y-component. Now because it has a y-component, it's gonna be adding to the normal force and these two together are going to compensate for the gravity downwards. And this friction force in the x-component... I haven't drawn things to scale here and this x-component is significantly larger to the left than this one is to the right because there is a net force horizontally here, there is acceleration— this car is accelerating towards the center but also moving along its curve at the same time though there has to be a net centripetal force in order for this car to go around the curve. So aside from that the drawing's good but just keep in mind that this x-component of normal force is meant to be longer than the x-component of friction. Okay! So considering the y-direction, I mentioned that the y-component of normal force plus y-component of friction upwards minus the gravity downwards, they have to balance and so their total is going to be zero. You know this is Newton's second law and here's mass times acceleration but there's no acceleration vertically and so we write zero here and then we can replace each of these terms by saying that the y-component of the normal force is F N times cos Θ because it's the adjacent leg of this right triangle and the friction force is the coefficient of static friction times the normal force but we want the y-component of it and so we multiply by sin Θ because this is the opposite leg of this triangle and then minus mg downwards all that equals 0. And that's about all we can do with this consideration of the y-direction and so then we have to turn our attention to the x-direction. Ultimately, we are solving for this by the way, that's our goal and right now, we have two unknowns: one being the normal force and the other being μ so that means we need a second equation. So we look at the x-direction and we say that... I have x going positive to the left, it's just the way I drew it and that's fine but just be aware that it's not your convention of having x positive to the right. So we have this normal force x-component positive to the left and then minus this x-component of friction which is negative to the right and this being the adjacent leg, you need to have cosine of Θ multiplied by the hypotenuse and the hypotenuse is μ sF N. So we have μ sF Ncos Θ is the x-component of friction and we have F N times sin Θ is the x-component of the normal force and all this equals mass times acceleration and there is acceleration in the x-direction— it is centripetal acceleration towards the center of the curve that the car is traveling in and that acceleration is v squared over r— so we replace 'a' there as well. So now we are gonna solve this for μ and so we'll add μ sF Ncos Θ to both sides and then we'll also subtract mv squared over r from both sides and then switch the sides around and we have this line here: μ sF Ncos Θ equals F Nsin Θ minus mv squared over r. And then divide both sides by these factors that are multiplying by the μ s and you get that the coefficient of static friction then is the normal force times sin Θ minus mv squared over r all divided by F Ncos Θ. Now this isn't the end of the story because we don't know what F N is so we are gonna make a substitution for F N and in preparation for that, let's clean things up a little bit— it's messy to have a fraction within a fraction— so let's divide both terms by this denominator and then that will make things a little bit simpler. So F Nsin Θ divided by F Ncos Θ is gonna be sin Θ over cos Θ because the F N's will cancel but then you have to divide this second term by F Ncos Θ as well and we'll have mv squared over F Nrcos Θ; nothing really changed except that the term became separated from this term here. And then sin Θ over cos Θ can be written more simply as tan Θ— that's a trigonometric identity that is worth memorizing. So now we have a formula for μ s here and F N appears only one place— that's nice— because if we are gonna substitute for it, we would like to have it in only do that substitution in only one place and we do know based on our work up here that the substitution's gonna be a little bit big. So let's return our attention to this y-direction and that is gonna reappear here where I did a little bit of work to it: I factored out the normal force and then moved the mg to the right hand side. So mg's on the right hand side, factored out the normal force and it's cos Θ plus μ ssin Θ and then divide both sides by this bracket and you get the normal force is mg over cos Θ plus μ ssin Θ. So that is what we are gonna substitute into F N in this formula for the coefficient of static friction. Now instead of putting this fraction in the denominator of this fraction— that's messy— we are gonna instead multiply this fraction by the reciprocal of the denominator. So dividing by something is the same as multiplying by its reciprocal so we can flip this fraction and multiply by it instead of dividing by it. So we have μ s equals tan Θ minus mv squared over rcos Θ and now here we have the multiplying by the flipped version of the normal force so that's cos Θ plus μ ssin Θ over mg and if you don't like this multiplying by the reciprocal, you don't have to you could substitute in this fraction as is into there if you like but I just think that's gonna be messy. Okay! So now our job is to collect the μ s together on one side... you see that this substitution introduced another instance of the variable we are trying to solve for so that means we have to do a bunch of algebra work to again isolate this μ s alone on one side. So let's divide the top's... there's two terms to consider here: there's mv squaredcos Θ and there's mv squaredμ ssin Θ. Those are two different terms you know, you get that after you distribute this into the brackets here keeping in mind that there's a minus there so this makes minus mv squaredcos Θ and minus mv squaredμ ssin Θ. Then you are dividing both those terms by mgrcos Θ but the m's cancel by the way so you don't have to worry about the m's actually. So we expect to have an rgcos Θ below both of our terms though and here we have rgcos Θ and we have rgcos Θ— so we are checking our work that's good— and then distribute the v squared into both terms and we have v squaredcos Θ—that's good— and we have v squared times μ ssin Θ and we have minuses in front of both of them. Alright and then cancel this cos Θ there and turn the sin Θ over cos Θ into a tan Θ and then move this term to the left side by adding it to both sides and we have μ s plus μ sv squaredtan Θ over rg equals tan Θ minus v squared over rg. And then I think another cleanup task is to get rid of all the fractions because they are gonna make things complicated looking so I'm going to multiply every single thing or both sides, in other words, by rg and this is just an aesthetic change; it's a personal preference, strategy to get rid of fractions because I don't wanna have fractions within fractions. Because we are gonna factor out the μ s here and then if we did it without doing the 'times rg', we would have μ s times 1 plus v squaredtan Θ over rg and then we would have to divide all this by that strange fraction. Okay! Anyway so we multiply both sides by rg that makes μ srg here, this term becomes μ sv squaredtan Θ because the rg's will cancel in that instance and here we have rgtan Θ minus v squared. Now we factor out the μ s from these two terms and so we have rg plus v squaredtan Θ leftover and then the right hand side is unchanged and then we divide both sides by this bracket and lastly, we have a formula for the coefficient of static friction: it's gonna be rgtan Θ minus v squared over rg plus v squaredtan Θ then we plug in numbers. So we have 100 meters times 9.80 meters per second squared times tan of 15.0 minus this slow speed of 5.5555 meters per second squared divided by 100 meters times 9.80 meters per second squared plus that speed squared times tan Θ, or tan 15.0, and we get 0.234 is the coefficient of static friction needed to prevent the car from slipping when they go at this speed slower than the ideal speed.